|
Question 1037369: two pipes running simultaneously can fill a tank in 2 hours and 40 minutes. after the large pipe had run for 3 hours the smaller pipe was also turned on and the tank was full 40 minutes later. how long would it take the smaller pipe to fill the tank alone?
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
two pipes running simultaneously can fill a tank in 2 hours and 40 minutes. after the large pipe had run for 3 hours the smaller pipe was also turned on and the tank was full 40 minutes later. how long would it take the smaller pipe to fill the tank alone?
Time smaller pipe takes, alone: 
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two pipes running simultaneously can fill a tank in 2 hours and 40 minutes.
After the large pipe had run for 3 hours the smaller pipe was also turned on and the tank was full 40 minutes later.
How long would it take the smaller pipe to fill the tank alone?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let L be the time (in hours) for Larger pipe to fill the tank alone, and
let S be the time (in hours) for Smaller pipe to fill the tank alone.
In one hour (in each hour) the larger pipe fills 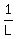 of the tank volume. It is the rate of the larger pipe.
In one hour (in each hour) the smaller pipe fills of the tank volume. It is the rate of the larger pipe.
In one hour (in each hour) the smaller pipe fills 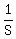 of the tank volume. It is the rate of the smaller pipe.
Working together, the two pipes fill of the tank volume. It is the rate of the smaller pipe.
Working together, the two pipes fill  of the tank volume. (So, the combined rate is the sum of the rates of individual pipes.)
We are given that in of the tank volume. (So, the combined rate is the sum of the rates of individual pipes.)
We are given that in   hours (=8/3 hours) the two pipes fill the tank working together. It means that hours (=8/3 hours) the two pipes fill the tank working together. It means that
 = = 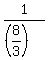 = = 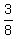 . (1)
Next, working for 3 hours, the larger pipe fills . (1)
Next, working for 3 hours, the larger pipe fills 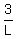 of the tank volume.
Also, in 40 minutes (= of the tank volume.
Also, in 40 minutes (= of an hour), two pipes working together fill of an hour), two pipes working together fill  of the tank volume.
And these two volumes are the entire tank volume: of the tank volume.
And these two volumes are the entire tank volume:
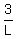 + +  = 1. (2)
Due to (1), we can rewrite (2) in the form = 1. (2)
Due to (1), we can rewrite (2) in the form
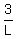 + +  = 1, or = 1, or 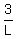 + + 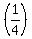 = 1.
This is an equation to determine L, and you can easily solve it: = 1.
This is an equation to determine L, and you can easily solve it: 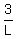 = =  and L = 4.
So, the larger pipe fills the tank in 4 hours.
Then from (1) and L = 4.
So, the larger pipe fills the tank in 4 hours.
Then from (1) 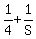 = = 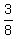 , , 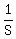 = =  and S = 8.
Answer. The smaller pipe fills the tank in 8 hours. and S = 8.
Answer. The smaller pipe fills the tank in 8 hours.
There is a block of lessons on joint work in this site
- Rate of work problems
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work
- Solving rate of work problem by reducing to a system of linear equations
- Selected joint-work word problems from the archive
- Joint work word problem for the day of April, 1
- Joint-work problems for 3 participants
- OVERVIEW of lessons on rate-of-work problems
Read them and become an expert in solution of rate-of-work and joint-work problems.
|
|
|
| |