SOLUTION: If bob and bill work together, they can do a job in 3h 44 min. If it takes Bob one hour more to the job than it takes Bill, find the time it would take each of them working alone

Algebra ->  Rate-of-work-word-problems -> SOLUTION: If bob and bill work together, they can do a job in 3h 44 min. If it takes Bob one hour more to the job than it takes Bill, find the time it would take each of them working alone      Log On


   

Question 1036910: If bob and bill work together, they can do a job in 3h 44 min. If it takes Bob one hour more to the job than it takes Bill,
find the time it would take each of them working alone to do the job.
Thank you.
Found 3 solutions by addingup, MathTherapy, ikleyn:
Answer by addingup(3677) About Me  (Show Source):
You can put this solution on YOUR website!
Hours to minutes: 3*60= 180 + 44 minutes = 224
224 = x+x+60
224= 2x+60
164 = 2x
x = 82
82/60 = 1.367 hours is what it takes Bill. And Bob?
1.37+1 = 2.37

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
If bob and bill work together, they can do a job in 3h 44 min. If it takes Bob one hour more to the job than it takes Bill, find the time it would take each of them working alone to do the job. 
Are you serious? How is it possible for 1 person to do a job (1 hr, plus) in FAR less time than it takes that person

and another to do the same job (matrix%281%2C2%2C+3%2611%2F15%2C+hours%29)? Are you kidding me? These people who're responding need to do FAR better.



Time Bill takes: highlight_green%28matrix%281%2C2%2C+7%2C+hours%29%29

Time Bob takes: 7 + 1, or highlight_green%28matrix%281%2C2%2C+8%2C+hours%29%29

Answer by ikleyn(52835) About Me  (Show Source):
You can put this solution on YOUR website!
.
If bob and bill work together, they can do a job in 3h 44 min. If it takes Bob one hour more to the job than it takes Bill,
find the time it would take each of them working alone to do the job.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

3 hours 44 minutes = 224 minutes.

Let x be the number of minutes (amount of time, in minutes) for Bill to complete the job working alone.

Then the number of minutes (amount of time, in minutes) for Bob to complete the job working alone is x + 60, according to the condition.

Working alone, Bill complete 1%2Fx of the job in one minute (in each minute). It is Bill's rate of work.

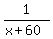Working alone, Bob complete 1%2F%28x%2B60%29 of the job in one minute (in each minute). It is Bob's rate of work.

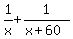Working together, Bob and Bill make 1%2Fx+%2B+1%2F%28x%2B60%29 of the job per minute. 
In other words, their combined rate of work is the sum of their individual rates.

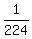From the other side, we know from the condition, that Bob and Bill make 1%2F224 of the job per minute working together.

So, we have this equation to determine x

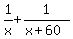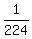1%2Fx+%2B+1%2F%28x%2B60%29 = 1%2F224.

To solve it, multiply both sides by 224*x*(x+60) to rid of denominators. You will get

224(x+60) + 224x = x*(x+60),  or

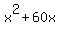448x + 13440 = x%5E2+%2B+60x,   or

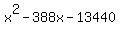x%5E2+-+388x+-+13440 = 0,

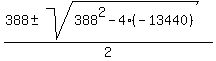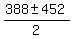x%5B1%2C2%5D = %28388+%2B-+sqrt%28388%5E2+-+4%2A%28-13440%29%29%29%2F2 = %28388+%2B-+452%29%2F2.


Only positive root is acceptable. It is x = 420 minutes,  or  x = 7 hours.


Answer.  Bill can complete the job in 7 hours working alone.
         Bob can do it in 8 hours working alone.