Question 1036850: HI,
How would I graph the solution set of the following system of linear inequalities in a Rectangular coordinate system. Show check points
2x+2y>6
x<5
y>= -2
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You would start by graphing the boundary lines for those inequalities are
 ,  , and  .
The solution to each inequality graphs as the half of the x-y plane to one side of the boundary line,
including or not including the boundary line.
The solution for  includes ,
the boundary line is part of the solution.
In the graph, that is indicated by drawing the line for as a solid line.
The other two inequalities do not have an equal sign, so their boundary lines
are not part of the solution,
and are graphed as dashed lines.
There is an easy way to figure out which side of a boundary line is part of the solution to an inequality.
All you have to do is to find a convenient "test point",
and see if it is a solution of the inequality.
The point (0,0), the origin, with  is often a convenient "test point".
The boundary lines and are easy to graph.
For , all you have to do is figure out that
when  ,  , so  and  ,
meaning that the point (0,3) is part of the graph, and that
when  ,  , so  and  ,
meaning that the point (3,0) is part of the graph.
Plotting those two points and connecting them with a straight line gives you the graph for .
The graph of the boundary lines should look like this:
 .
Then using the test point (0,0), with , you realize that
since  , (0,0) is a solution of .
So, the graph of is the line plus
all the space above that line (on the same side as the origin.
Also using the test point (0,0), you realize that
since  , (0,0) is a solution of  .
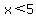So, the graph of 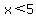is the side of the line that contains the point (0,0),
meaning all the space to the left of the dashed line  .
Finally, using the test point (0,0), you realize that
since for ,  ,
the point (0,0) is not a solution of  .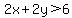
So, the graph of 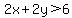is the side of the line that does not contain the point (0,0),
meaning all the space to the right/above of the dashed line .
The solution to 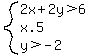 is the part of the plane
that is the solution to all three inequalities at the same time,
graphed as the shaded wedge between the two dashed lines:
 .
|
|
|
