Question 1036737: In an arithmetic progression, the thirteenth term
Is 27, and the seven term is three times the second term.find the first term and the common differences.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In an arithmetic progression, the thirteenth term
is 27, and the  seventh term is three times the second term. seventh term is three times the second term.
Find the first term and the common differences.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We are given
 = 27, (1) = 27, (1)
 = = 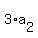 . (2)
which, in other terms, is . (2)
which, in other terms, is
 + 12*d = 27, (1') + 12*d = 27, (1')
 + 6*d = + 6*d = 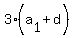 . (2').
Simplify it and write in the canonical form for the system of two equations in two unknowns: . (2').
Simplify it and write in the canonical form for the system of two equations in two unknowns:
 + 12*d = 27, (1'') + 12*d = 27, (1'')
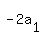 + 3*d = 0. (2'')
Now, based on (2''), replace the term 12*d in (1'') by + 3*d = 0. (2'')
Now, based on (2''), replace the term 12*d in (1'') by 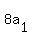 . You will get a single equation for . You will get a single equation for 
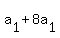 = 27, or = 27, or 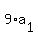 = 27, which gives you = 27, which gives you  = 3.
Then from (2'') 3d = = 3.
Then from (2'') 3d = 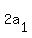 = 6. Hence, d = 2.
Answer. = 6. Hence, d = 2.
Answer.  = 3, d = 2. = 3, d = 2.
|
|
|