Question 1036606: Hi !
I am having difficulties with this problem, we do not get along.
We have a 20% alcohol solution and a 50% solution. How many pints must be used from each to obtain 8 pints of a 30% solution ?
Set up and solve using a system of algebraic equation.
Thank you so much
Found 2 solutions by jorel555, ikleyn:
Answer by jorel555(1290)   (Show Source):
You can put this solution on YOUR website! Let n be the amount of 50% solution. Then:
n(.50)+(8-n)(.20)=8(.3)
.5n-.2n+1.6=2.4
.3n=.8
n=.8/.3=2.67 pints of 50% solution; 5.33 pints of 20% solution!!!!!!!!!!!!!
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Hi !
I am having difficulties with this problem, we do not get along.
We have a 20% alcohol solution and a 50% solution. How many pints must be used from each to obtain 8 pints of a 30% solution ?
Set up and solve using a system of algebraic equation.
Thank you so much
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let n be the number of pints of the 20% alcohol solution needed, and
let m be the number of pints of the 50% alcohol solution needed.
Then the total volume equation is
n + m = 8. (1)
n pints of the 20% alcohol solution contain 0.2n pints of the pure alcohol.
m pints of the 50% alcohol solution contain 0.5m pints of the pure alcohol.
In total, the mixt contains 0.2n + 0.5m pints of the pure alcohol.
So, the second equation for the alcohol percentage/contents in the mixt is
 = 0.3.
You can rewrite the last equation in the form
0.2n + 0.5m = 0.3*8, or
0.2n + 0.5m = 2.4. (2)
These two equations, (1) and (2), form the system of two linear algebraic equations in two unknowns, n and m.
There are many ways to solve it. You can use the Substitution method, for example.
For it, express x from (1) as n = 8-m and substitute it into (2). You will get
0.2*(8-m) + 0.5m = 2.4,
1.6 -0.2m + 0.5m = 2.4,
0.3m = 2.4 - 1.6 = 0.8,
m = 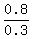 =   pint.
Then n = 8 - m =   pint.
Answer. pint of the 20% alcohol solution and pint of the 50% alcohol solution.
|
|
|
