.
Please help me solve this question
If alpha and beta are 2 positive acute angles satisfying alpha - beta = 15 degree and sin alpha = cos 2 beta then find value of alpha + beta
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If  =
= 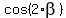 , then
, then
 =
= 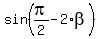 .
Due to constrains imposed on
.
Due to constrains imposed on  and
and  , it implies that
, it implies that
 =
=  , or
, or
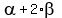 =
=  . (1)
From the condition, we also have the second equation
. (1)
From the condition, we also have the second equation
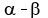 =
= 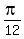 . (2) (
. (2) ( 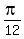 = 15 degs)
Distract equation (2) from (1) (both sides). You will get
= 15 degs)
Distract equation (2) from (1) (both sides). You will get
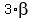 =
= 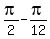 =
= 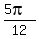 .
Hence,
.
Hence,  =
= 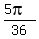 =
= 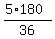 = 5*5 = 25 degs.
Then
= 5*5 = 25 degs.
Then  =
=  =
=  =
= 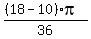 =
= 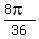 =
=  = 40 degs.
Answer.
= 40 degs.
Answer.  =
=  = 40 degs;
= 40 degs;  =
= 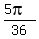 = 25 degs.
= 25 degs.