Question 1036508: I am really having a hard time with this one. Been working on it for nearly 3 hours and cant seem to figure out how to make it work.
Problem: r(t) is the position of a particle in the xy-plane at time t. Find an equation in x and y whose graph is the path of the particle. Then find the particle’s velocity and acceleration vectors at the given value of t.

where 
To find the Equation, I first organize it into a set:
[ 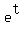 , , 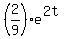 ] ]
Then I just plug in the value of t (ln3)
[  , , 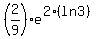 ] ]
I then reconstruct the original problem with the new values:


then I change the i / j coordinates to x/y coordinates

-----------------------------
As for velocity and acceleration, so far I have figured it like this:
Velocity:
[ 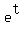 , , 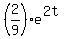 ] ]
[ 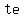 , , 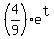 ] ]

Acceleration:
[ 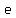 , , 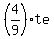 ] ]

Am I taking the derivative correctly? As far as I know, e remains as e, even after the derivative, right?
thanks in advance
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|