Question 1036430: Evaluate the expression under the given conditions
sin(θ − ϕ); tan θ = 12/5, θ in Quadrant III, sin ϕ = -(sqrt 10)/10 , ϕ in Quadrant IV
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Evaluate the expression under the given conditions
sin(θ − ϕ); tan θ = 12/5, θ in Quadrant III, sin ϕ = -(sqrt 10)/10 , ϕ in Quadrant IV
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
To evaluate 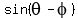 you will use the formula you will use the formula
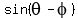 = = 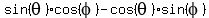 . (1)
To use this formula, you need to know . (1)
To use this formula, you need to know  , , 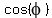 , ,  and and 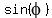 .
Is it given to you? - Only in part: you are given " .
Is it given to you? - Only in part: you are given "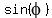 = =  and and 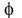 is in Q4".
Regarding is in Q4".
Regarding  , you are given that " , you are given that " = =  and and  is in Q3".
So, your first task is, based on the given data, find is in Q3".
So, your first task is, based on the given data, find  , ,  and and 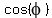 .
You have .
You have  = = 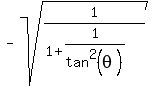 = = 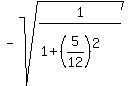 = = 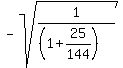 = = 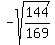 = = 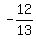 .
The sign "-" was chosen for the square root, because the sine is negative for an angle in Q3.
Having .
The sign "-" was chosen for the square root, because the sine is negative for an angle in Q3.
Having  = = 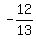 , you can easily calculate , you can easily calculate
 = = 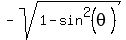 = = 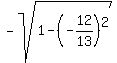 = = 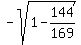 = = 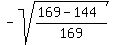 = = 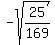 = = 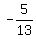 .
The sign "-" was chosen for the square root, because the cosine is negative for an angle in Q3.
Next, .
The sign "-" was chosen for the square root, because the cosine is negative for an angle in Q3.
Next, 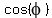 = = 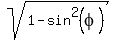 = = 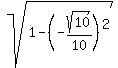 = =  = = 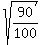 = = 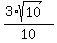 .
The sign "+" was chosen for the square root, because the cosine is positive for an angle in Q4.
Let us summarize what we have so far: .
The sign "+" was chosen for the square root, because the cosine is positive for an angle in Q4.
Let us summarize what we have so far:  = = 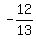 , , 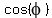 = = 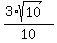 , ,  = = 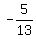 and and 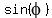 = =  .
Now you can plug-in this data into the formula (1) and get .
Now you can plug-in this data into the formula (1) and get
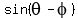 = =  = = 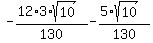 = = 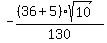 = = 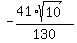 .
Answer. .
Answer. 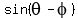 = = 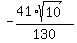 . .
For many other similar problems see the lessons
- Calculating trigonometric functions of angles
- Advanced problems on calculating trigonometric functions of angles
in this site.
|
|
|