Question 1036364: Find three consecutive even integers such that four times the first equals 16 times the sum of the third and the number two.
Thank you! I simply don't know where to start or what to do :)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE ALGEBRA WAY:
Start by calling the three consecutive even integers
 , ,  , and , and  , or , or
 , ,  , and , and  . .
Then, find expressions for:
"four times the first" = , ,
"the sum of the third and the number two" =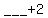 , ,
and "16 times" that sum =  . .
Finally write an equation that says that
the expression for "four times the first"
equals the expression for
"16 times the sum of the third and the number two".
When you solve that equation,
you should find an  that is an even integer. that is an even integer.
If the  you find is not an even integer, you find is not an even integer,
either you made a mistake in your calculations,
or there is no solution to the problem.
THE FIFTH GRADER ANSWER:
The problem says "integers", meaning "whole numbers",
so  , ,
and negative numbers, such as  , could be involved. , could be involved.
Let us use some educated guess and check,
picking a first set of "three consecutive even integers,
and then a second set of "three consecutive even integer";
seeing how far away "four times the first" is from
"16 times the sum of the third and the number two",
and deciding which way to move to choose the next set.
First try: 2, 4, and 6. With that choice,
"four times the first" =  , ,
"16 times the sum of the third and the number two" = . .
The two expressions are  apart. apart.
Second try: 8, 10, and 12. With that choice,
"four times the first" =  , ,
"16 times the sum of the third and the number two" = . .
The two expressions are  apart. apart.
Since choosing the even integers so that they were more than 2, 4, and 6 made the difference greater (worse),
let us pick integers that are less than 2, 4, and 6.
How about 0, 2,and 4? With that choice,
"four times the first" =  , ,
"16 times the sum of the third and the number two" = . .
The two expressions are  apart. apart.
The different got smaller, so we are getting warmer
How about -4, -2,and 0? With that choice,
"four times the first" =  , ,
"16 times the sum of the third and the number two" = . .
The two expressions are  apart, and apart, and
"16 times the sum of the third and the number two"
is still more that "four times the first".
How about -8, -6,and -4? With that choice,
"four times the first" =  , ,
"16 times the sum of the third and the number two" = , ,
and we have hit the jackpot:
the solution is  , , 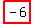 , and , and  . .
NOTE 1:
When looking for consecutive even integers, or consecutive odd integers,
you do not need to get complicated with the expressions for each integer.
Just call one of those integers  or or  , ,
and the others have to be  apart, as in apart, as in
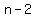 , ,  , and , and  . .
You will either find the kind of integer (even or odd) that you need for the answer,
or you will find something unexpected, and will have to figure out if it is your mistake, or a tricky problem without a valid solution.
NOTE 2:
The fifth grader probably does not know it, but the fifth grader's strategy works only because both expressions are simple linear expressions.
If there was a "squared" in one of those expressions, it may not work.
Anyway, the fifth grader got to the solution fairly easily, didn't she?
|
|
|