|
Question 1036325: Solve for x and y:
2x-7y=-1
3x-2y=7
My problem is that the signs are the same for both variables so I really don't know what to do! Please help me, how many methods are there?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equations are:
2x - 7y = -1
3x - 2y = 7
there are 3 basic methods.
you can find them in this tutorial.
http://www.purplemath.com/modules/systlin1.htm
there are 7 pages to the tutorial, so go through them all.
the last method they discuss (gaussian elimination), you probably won't need for a while.
the three main methods you will probably use are elimination and substitution and graphing.
i'll take you through those.
substitution.
in this method, you solve for one of the variables in one equation and use the value obtained to replace one of the variables in the other equation.
your two equations are:
2x - 7y = -1
3x - 2y = 7
solve for y in the first equation as follows:
2x - 7y = -1
subtract 2x from both sides of this equation to get - 7y = -2x - 1
divide both sides of this equation by -7 to get y = -2/-7 * x - 1/-7.
simplify this to get y = 2/7 * x + 1/7
now replace y with 2/7 * x + 1/7 in the second equation and solve for x.
start with 3x - 2y = 7
replace y with 2/7 * x + 1/7 to get 3x - 2 * (2/7 * x + 1/7) = 7
simplify to get 3x - 4/7 * x - 2/7 = 7
multiply both sides of the equation by 7 to get rid of the fractions.
you will get 21x - 4x - 2 = 49
add 2 to both sides of the equation and combine like terms to get 17x = 51.
divide both sides of the equation by 17 to get x = 3.
now go back to the first equation and solve for y.
the first equation is 7y = 2x + 1
when x = 3, this becomes 7y = 6 + 1
simplify to get 7y = 7
divide both sides of the equation by 7 to get y = 1
your solutions should be x = 3 and y = 1
those values should satisfy both equations, which they do, because i went back and evaluated both equations using x = 3 and y = 1 and confirmed that those equations are true when x = 3 and y = 1.
your next method is elimination, which may be the one you tried and had a problem with.
the two equations are:
2x - 7y = -1
3x - 2y = 7
you need to multiply both sides of one or both of the equations so that one of the variables will cancel out when you add the equations together or subtract one of the equations from the other.
you will be left with one variable in one equation which you can solve, and then go back and solve for the other.
i looked at the equations and determined that if i multiply the first equation by 3 and the second equation by 2, then i should be able to cancel out the x and then solve for y.
so, i multiply both sides of the first equation by 3 and both sides of the second equation by 2 to get:
2x - 7y = -1
3x - 2y = 7
becomes:
6x - 21y = -3
6x - 4y = 14
if i add these equations together, i won't be able to cancel the x variable.
however, if i subtract one of the equations from the other i will.
subtracting one equation from the other is the same as multiplying both sides of one of the equations by -1 and then adding them together.
i will multiply both sides of the second equation by -1 and leave the first equation alone to get:
6x - 21y = -3
-6x + 4y = -14
now, when i add both equations together, i get -17y = -17
i solve for y and get y = 1.
now that i know that y = 1, i use one of the equations to solve for x.
i'll use the first to get 6x - 21 = -3
add 21 to both sides of this equation to get 6x = 18.
solve for x to get x = 3.
same answer as before.
x = 3
y = 1
solve by graphing involves graphing both equations and then looking for the intersection.
in most cases, you will need to solve for y in order to be able to graph them.
the two equations are:
2x - 7y = -1
3x - 2y = 7
solve for y in 2x - 7y = -1 to get y = (-2x -1)/-7
solve for y in 3x - 2y = 7 to get y = (-3x+7)/-2
the graphing software will take care of the rest.
if the lines intersect, you will have a solution.
that solution will be the intersection point of the lines.
my graph is shown below.
you can see that the intersection point has an x-coordinate of 3 and a y-coordinate of 1.
that's the solution that is common to both equations.
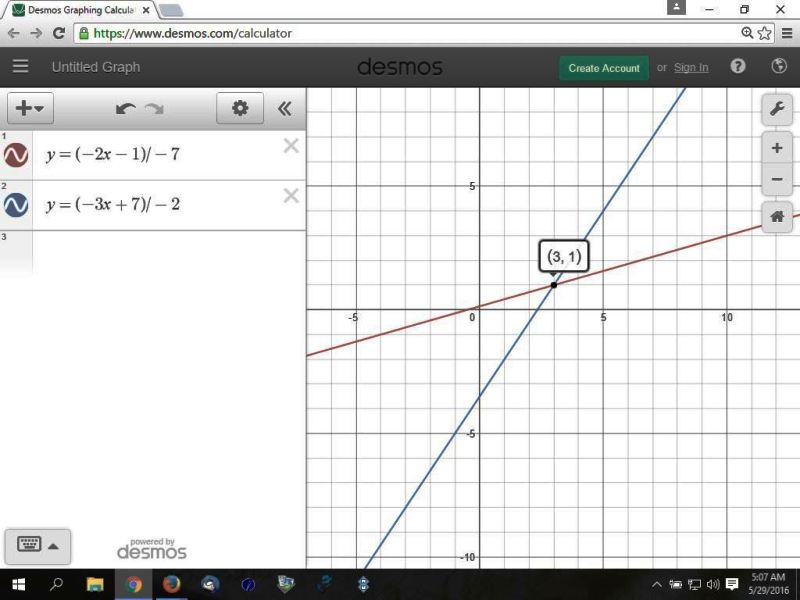
if the lines are parallel (they have the same slope and a different y-intercept), then there will be no solution because the lines will never instersect.
if the lines are identical (they have the same slope and the same y-intercept), then there will be an infinite number of solutions because they are essentially the same line.
to figure out whether they are identical or parallel, you need to convert the linear equation to slope intercept form.
slope intercept form is y = mx + b, where m is the slope and b is the y-intercept.
converting to slope intercept form is basically solving for y and then re-ordering the terms in descending order of degree and simplifying as much as possible.
when you solved for y in both equations so you could graph them, you got:
y = (-2x-1)/-7
y = (-3x+7)/-2
those equations are solved for y, but they are not in slope intercept form.
take y = (-2x - 1) / -7 and simplify to get y = (2/7) * x + (1/7).
take y = (-3x + 7) / -2 and simplify to get y = (3/2) * x - (7/2).
these are the same equations, but now they are in slope intercept form.
since the slope of each equation is different from the other, they are not parallel or identical and you will have a solution.
in fact, you did.
it was x = 3 and y = 1.
|
|
|
| |