SOLUTION: sin(3x)+cos(3x) = -1 solve for x.

Algebra ->  Trigonometry-basics -> SOLUTION: sin(3x)+cos(3x) = -1 solve for x.      Log On


   

Question 1036275: sin(3x)+cos(3x) = -1 solve for x.
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
sin(3x) + cos(3x) = -1 solve for x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

sin(3x) + cos(3x) = -1.    (1)   (It is the original equation)

Square its both sides. You will get

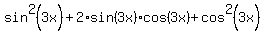sin%5E2%283x%29+%2B+2%2Asin%283x%29%2Acos%283x%29+%2B+cos%5E2%283x%29 = 1.   (2)

From the other side, there is an identity

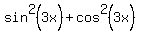sin%5E2%283x%29+%2B+cos%5E2%283x%29 == 1.   (3)

Comparing (2) and (3), you get

2*sin(3x)*cos(3x) = 0,   or  sin(3x)*cos(3x) = 0.    (4)

Equation (4) splits in two independent equations

1)  sin(3x) = 0  --->  3x = k%2Api,   k = 0. +/-1. +/-2, . . . 
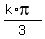                 --->   x = %28k%2Api%29%2F3,  k = 0, +/-1. +/-2, . . .       (5)

2)  cos(3x) = 0  --->  3x = pi%2F2+%2B+k%2Api,   k = 0. +/-1. +/-2, . . . 
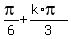                 --->   x = pi%2F6+%2B+%28k%2Api%29%2F3,  k = 0. +/-1. +/-2, . . .   (6)

Now we should check which of the found values (5), (6) satisfy the original equation.

Of the set (5), all x satisfy sin(3x) = 0. Hence, only those of (5) satisfy the original equation where cos(3x) = -1.
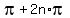They are  3x = pi+%2B+2n%2Api,    n = 0, +/-1. +/-2, . . . ,  or 

           x = %28%282n%2B1%29%2F3%29%2Api,  n = 0, +/-1. +/-2, . . . ,           (5').

Of the set (6), all x satisfy cos(3x) = 0. Hence, only those of (6) satisfy the original equation where sin(3x) = -1.
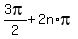They are  3x = 3pi%2F2+%2B+2n%2Api,   n = 0, +/-1. +/-2, . . . ,  or 

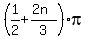           x = %281%2F2%2B%282n%29%2F3%29%2Api,  n = 0, +/-1. +/-2, . . . ,           (6'). 

Answer.  The union of the sets (5') and (6') is the solution of the original equation.