SOLUTION: there are 5 sacks, and they are weighed 2 at a time. Their weights are 11,11.2,11.3,11.4,11.5,11.6,11.7,11.8,12 and 12.1. This is the weight of all the possible outcomes. How heavy

Let us call these sacks by the names "a", "b", "c", "d" and "e".

And let "a" be the lightest, "b" is the next by the weight, "c" is the next after "b", "d" is next after "c", and "e" is 
the next after "d" (and the last).

Since all 10 given outcomes are different numbers, all "a, "b", "c", "d" and "e" have different weights. 
Had some of the sacks have equal weight, some numbers in the outcome data would be equal, which is not the case.

If you add all outcomes, you will get the sum 

11 + 11.2 + 11.3 + 11.4 + 11.5 + 11.6 + 11.7+ 11.8 + 12 + 12.1 = 115.6.

It is the sum of all pairs (a+b), (a+c), (a+d), . . . , (d+e) taken 2 at a time. By grouping and regrouping,
you can easily understand that it is nothing else as 4*(a+b+c+d+e), i.e four times the sum of (a+b+c+f+e).

It implies that the sum

a + b + c + d + e = 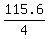 = 28.9.   (1)

Now, it is clear that the very first outcome 11 (the smallest outcome) is the sum of "a and "b", the two lightest sacks. 
It can not be nothing else. So, we have 

a + b = 11.      (2)

Similarly, it is clear that the very next outcome  11.2  is the sum of "a" and "c". It simply can not be nothing else. So, we have 

a + c = 11.2.    (3)


Next, it is clear that the very last outcome 12.1 (the greatest outcome) is the sum of "d" and "e", the two heaviest sacks. 
It can not be nothing else. So, we have 

d + e = 12.1.    (4)

Similarly, outcome  12  is the sum of "c" and "e". It simply can not be nothing else. So, we have 

c + e = 12.      (5)


Take the sum of (2) and (3). You will get

a + b + d + e = 11 + 12.1 = 23.1.   (6)

Now distract (6) from (1). You will get

c = 28.9 - 23.1 = 5.8.

So, we just found "c".


Now we can easily find all remaining unknowns.

From (3),  a = 11.2 - c = 11.2 - 5.8 = 5.4.

From (2),  b = 11   - a = 11   - 5.4 = 5.6.

From (5),  e = 12   - c = 12   - 5.8 = 6.2.

From (4),  d = 12.1 - e = 12.1 - 6.2 = 5.9.


Answer. The sacks are 5.4, 5.6, 5.8, 5.9 and 6.2, from lightest to heaviest.