Question 1035865: Susan borrowed $5000. The terms of the loan were equal monthly payments at Susan 12% compounded monthly for 3 ysears. After making payments for 1 year,Susan decided to pay off the balance of the loan. A) what was susans monthly payment.B) how much must Susan pay at the end of 1 year to pay off the balance of the loan.C)How much interest did Susan save by repaying the loan in 1 year.
Found 2 solutions by Aldorozos, MathTherapy:
Answer by Aldorozos(172)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two ways to solve this problem. One is to use the Future Value problem. It is time consuming to solve it this in this format. One easy way to solve this problem is to use Amortization Table. If you go to the following site http://www.calculator.net/amortization-calculator.html
and put the information: this is what you get:
Beginning Balance Interest Principal Ending Balance
1 $5,000.00 $50.00 $116.07 $4,883.93
2 $4,883.93 $48.84 $117.23 $4,766.70
3 $4,766.70 $47.67 $118.40 $4,648.29
4 $4,648.29 $46.48 $119.59 $4,528.70
5 $4,528.70 $45.29 $120.78 $4,407.92
6 $4,407.92 $44.08 $121.99 $4,285.93
7 $4,285.93 $42.86 $123.21 $4,162.71
8 $4,162.71 $41.63 $124.44 $4,038.27
9 $4,038.27 $40.38 $125.69 $3,912.58
10 $3,912.58 $39.13 $126.94 $3,785.63
11 $3,785.63 $37.86 $128.21 $3,657.42
12 $3,657.42 $36.57 $129.50 $3,527.92
year 1 end
13 $3,527.92 $35.28 $130.79 $3,397.13
14 $3,397.13 $33.97 $132.10 $3,265.03
15 $3,265.03 $32.65 $133.42 $3,131.61
16 $3,131.61 $31.32 $134.75 $2,996.85
17 $2,996.85 $29.97 $136.10 $2,860.75
18 $2,860.75 $28.61 $137.46 $2,723.29
19 $2,723.29 $27.23 $138.84 $2,584.45
20 $2,584.45 $25.84 $140.23 $2,444.22
21 $2,444.22 $24.44 $141.63 $2,302.59
22 $2,302.59 $23.03 $143.04 $2,159.55
23 $2,159.55 $21.60 $144.47 $2,015.07
24 $2,015.07 $20.15 $145.92 $1,869.15
year 2 end
25 $1,869.15 $18.69 $147.38 $1,721.77
26 $1,721.77 $17.22 $148.85 $1,572.91
27 $1,572.91 $15.73 $150.34 $1,422.57
28 $1,422.57 $14.23 $151.84 $1,270.73
29 $1,270.73 $12.71 $153.36 $1,117.36
30 $1,117.36 $11.17 $154.90 $962.46
31 $962.46 $9.62 $156.45 $806.02
32 $806.02 $8.06 $158.01 $648.01
33 $648.01 $6.48 $159.59 $488.41
34 $488.41 $4.88 $161.19 $327.23
35 $327.23 $3.27 $162.80 $164.43
36 $164.43 $1.64 $164.43 $0.00
year 3 end
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! Susan borrowed $5000. The terms of the loan were equal monthly payments at Susan 12% compounded monthly for 3 ysears. After making payments for 1 year,Susan decided to pay off the balance of the loan. A) what was susans monthly payment.B) how much must Susan pay at the end of 1 year to pay off the balance of the loan.C)How much interest did Susan save by repaying the loan in 1 year.
Monthly payment made = 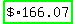 , using the payment formula, based on the present value of an ordinary annuity. , using the payment formula, based on the present value of an ordinary annuity.
This is:  , where: , where:
PMT = Monthly payment (unknown in this case)
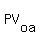 = Present Value of an Ordinary Annuity ($5,000, in this case) = Present Value of an Ordinary Annuity ($5,000, in this case)
i = Annual Interest Rate (12%, or .12, in this case)
m = Compounding periods, per year (Monthly, or 12, in this case)
t = Time, in years (3, in this case)
Calculating the amortization on this loan results in a total payment, in 1 year, of $1,992.86, of which $520.78 was applied to interest, and $1,472.08 applied to principal.
The payoff amount, after 1 year then, was: $5,000 - $1,472.08, or 
If she'd continued to pay $166.07 over the 3-year period, she would've paid a total of $5,978.58, of which $978.58 would've been applied to interest.
By the time the loan was paid off (1 year's time), she'd paid $520.78 in interest. If she'd continued for the 3 years, she would've had to pay $978.58 in interest.
Therefore, she saved: $978.58 - 520.78, or  , in interest. , in interest.
|
|
|