SOLUTION: In a triangle ABC ,AB=12cms , BC=8cms, CA=10cms .An incircle is drawn inside the triangle touching the sides AB,BC and CA at the points D,E and F respectively. Find AF, BD, and C

  

  

I have found an appropriate figure from my archive  (see on the right).
Although it is not in the scale, it is not so important for the solution.                 

The names a, b and c are just employed for the side lengths:
|AB| = c = 12 cm, |BC| = a = 8 cm, and |AC| = b = 10 cm.

So we introduce d = |AD|= |AF|, e = |BE| = |BD| and f = |CF| = |CE|.

I hope you are familiar with the fact that tangent lines to a circle drawn 
from the outside point, are congruent, and therefore doubled equalities 
in the line above do not arose questions.

We have this system of equations

|AD| + |BD| = |AB|,                                 d + e = a,    (1)
|BE| + |CE| = |BC|,       or, which is the same,    e + f = b.    (2)
|AF| + |CF| = |AC|                                  d + f = c.    (3)

By adding equations (1), (2) and (3), you get

2(d + e + f) = a + b + c,   or    d + e + f = .     (4)
 
  


 
 
Now distract equation (1) from (4).         You will get  f = 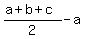 = 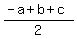.    (5)

Next, distract equation (2) from (4).       You will get  d = 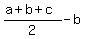 = 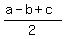.     (6)

Similarly, distract equation (3) from (4).  You will get  e = 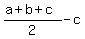 = .     (7)

Now substitute (plug in) the given numerical data into equations (5), (6) and (7). You will get

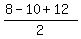f =  = 7 cm,  d =  = 5 cm, e =  = 3 cm.

Answer.  AF = d = 5 cm,  BD = e = 3 cm, and CE = f = 7 cm.