SOLUTION: Segment RS is an altitude of triangle PQR. Find the area of the triangle. Triangle PQR with altitude RS is shown. Point P is at negative 2, 1. Point Q is at 6, 1. Point R is at

Algebra ->  Length-and-distance -> SOLUTION: Segment RS is an altitude of triangle PQR. Find the area of the triangle. Triangle PQR with altitude RS is shown. Point P is at negative 2, 1. Point Q is at 6, 1. Point R is at       Log On


   

Question 1035507: Segment RS is an altitude of triangle PQR. Find the area of the triangle.
Triangle PQR with altitude RS is shown. Point P is at negative 2, 1. Point Q is at 6, 1. Point R is at 4, negative 3. Point S is at 4, 1.
15.5
16
17.5
18
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
With 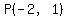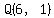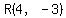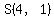P%28-2%2C1%29 , Q%286%2C1%29 , R%284%2C-3%29 , S%284%2C1%29 ,
the red%28triangle%29 and its green%28altitude%29 look like this:

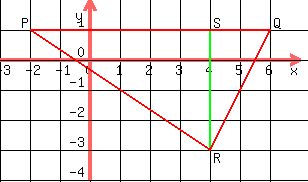
The length of base PQ is the difference in the x-coordinates of P and Q,
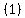6-%28-2%29=6%2B2=8 , because the y-coordinates are both the same, %281%29 .
The height (the length of altitude RS is the difference in the y-coordinates of R and S,
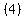1-%28-3%29=1%2B3=4 , because the y-coordinates are both the same, %284%29 .
The area is
base%2Aheight%2F2=8%2A4%2F2=highlight%2816%29 .