SOLUTION: Find the vertex, focus, and directrix of the parabola with equation y=x^2+6x+5

Since the coefficient of x2 is positive,
we know that the parabola opens upward.

We must get it into the form:



where (h,k) is the vertex and p is the number of units
the vertex is from both the focus (point) and the 
directrix (line).



Get the x terms on the left and other terms on the right



Multiply through by -1



Complete the square on the left:
1. Multiply the coefficient of x by 1/2, getting 6(1/2) = 3
2. Square the result of step 1, getting +9
3. Add +9 to both sides 



Factor the left side, combine like terms on the right:



Write (x+3)(x+3) as (x+3)2



Factor out 1 on the right to show the value of 4p



Compare to



-h=+3 so h=-3
4p=1 so p=1/4
-k=+4 so k=-4

Vertex = (h,k) = (-3,-4)

We can easily get the intercepts from
the original equation.




So the x-intercepts are (-5,0) and (-1,0)

To get the y-intercept:





So the y-intercept is (0,5), so we draw
the graph:



The focus is the point which is  of a unit above the
vertex, and the directrix is a line  of a unit below
the vertex. I'll make them green:



Since the focus (the green point) is p=1/4 of a unit above 
the vertex (-3,-4), the focus has the same x-coordinate as 
the vertex, and the y-coordinate is 1/4 of a unit above the 
the y-coordinate of the vertex. So we add 1/4 to the y-coordinate 


So the focus (the green point) is the point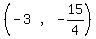 

The directrix (the green line) is a horizontal line which is
1/4 of a unit below the y-coordinate of the vertex, so we subtract
1/4 from the y-coordinate of the vertex to find out how far below
the x-axis the directrix is.


So the directrix is the horizontal line which has the equation:


   
Edwin