Question 1035228: A binomial experiment has 5 trials in which p = 0.7. What is the probability of getting at least 2 successes?
my equation I came up with is p(0)+p(1)=5c0(.4)^0(.6)^5-0+5c1(.4^1(.6)^5-0
Found 2 solutions by stanbon, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A binomial experiment has 5 trials in which p = 0.7. What is the probability of getting at least 2 successes?
P(2<= x <=5) = 1 - p(0<= x <=1) = 1 - binomcdf(5,0.7,1) = 1-0.0308 = 0.9692
------
Cheers,
Stan H.
-------------
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! A binomial experiment has 5 trials in which p = 0.7. What is the probability of getting at least 2 successes?
my equation I came up with is p(0)+p(1)=5c0(.4)^0(.6)^5-0+5c1(.4^1(.6)^5-0
I don't know where you got .4 from. The probability of SUCCESS (p) is .7, not .4.
You also had the right idea, it appears, in determining the probability of getting @ MOST 1, which is:
 , but then to get @ least 2, which is the SUM of P(2) through P(5), , but then to get @ least 2, which is the SUM of P(2) through P(5),
cumulative, you'd need to subtract this probability from 1.
We then get: 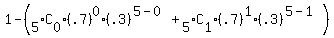 = 1 - .0308 = = 1 - .0308 = 
If you're familiar with MS Excel, you could use 1 - BINOMDIST to get this probability
If you're familiar with the TI-83/84 calculator, you could use: BINOMCDF to get this probability
|
|
|