|
Question 1035164: A chef is using a mixture of two brands of Italian dressing. The first brand contains 6% vinegar, and the second brand contains 11% vinegar. The chef wants to make 210 milliliters of a dressing that is 8% vinegar. How much of each brand should she use?
Found 2 solutions by ikleyn, jorel555:
Answer by ikleyn(52797)   (Show Source):
You can put this solution on YOUR website! .
A chef is using a mixture of two brands of Italian dressing. The first brand contains 6% vinegar, and the second brand
contains 11% vinegar. The chef wants to make 210 milliliters of a dressing that is 8% vinegar. How much of each brand should she use?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
x + y = 210, (1)
0.06*x + 0.11*y = 0.08*210, (2)
Multiply (1) by 100 and simplify. You will get the modified system
x + y = 210, (1')
6*x + 11*y = 1680. (2')
Solve it by using the Substitution method.
From (1') express x = 210 - y and substitute into (2'). You will get a single equation
6*(210-y) + 11y = 1680,
1260 - 6y + 11y = 1680,
5y = 1680-1260,
5y = 420,
y = 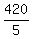 = 84.
Answer. 84 milliliters of the 11% vinegar and 210-84 = 126 milliliters of the 6% vinegar.
Check. 0.06*126 + 0.11*84 = 16.80. Correct!
Answer by jorel555(1290)  (Show Source):
You can put this solution on YOUR website! Let n be the amount of 6% mixture:
.06(n)+.11(210-n)=.08(210)
.06n+23.1-.11n=16.8
.05n=6.3
n=6.3/.05=126ml of .06 mixture, and 84 ml of .11 mixture needed!!!!!!!!!
|
|
|
| |
