Question 1035084: Elaine has 88 coins in a purse which are all 5-cent coins and 10-cent coins. The total value of the coins are $7. How many of each type of coin does she have
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52860)   (Show Source):
You can put this solution on YOUR website! .
Elaine has 88 coins in a purse which are all 5-cent coins and 10-cent coins. The total value of the coins are $7.
How many of each type of coin does she have?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let n be the number of nickels (5-cent coins) Elain has.
Then the number of dimes (10-cent coins) is (88-n).
n nickels contribute 5n cents into the total.
(88-n) dimes contribute 10*(88-n) cents into the total.
So, you have this "value" equation
5n + 10*(88-n) = 700 cents.
Simplify and solve:
5n + 880 - 10n = 700, or
-5n = 700 - 880,
-5n = -180,
n = 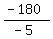 =  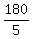= 36.
So, Elaine has 36 nickels (5-sent coins) and 88-36 = 52 dimes (10-cent coins).
Check. 5*36 + 10*52 = 180 + 520 = 700 cents. Correct!
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! x = number of 10 cent coins.
y = number of 5 cent coins.
10 * x = total number of cents in x number of 10 cent coins.
5 * y = total number of cents in y number of 5 cent coins.
since you are dealing in cents, then you need to convert everything to cents.
dollars * 100 = cents.
7 dollars is equal to 700 cents.
total number of coins is 88, so you get x + y = 88.
total value in cents is equal to 700, so you get 10x + 5y = 700.
you have 2 equations that need to be satisfied simultaneously.
they are:
x + y = 88
10x + 5y = 700
if you multiply both sides of the first equation by 10 and leave the second equation as is, you get:
10x + 10y = 880
10x + 5y 700
if you subtract the second equation from the first, you get:
5y = 180.
divide both sides of this equation by 5 to get:
y = 36.
since x + y = 88, then x = 88 - 36 = 52.
since x = 52 and y = 36, you get:
10x + 5y = 10*52 + 5*36 = 520 + 180 = 700.
the solution looks good.
you have 52 ten cent coins and you have 36 five cent coins.
their sum is 700 cents which is equal to 7 dollars.
|
|
|
