SOLUTION: Train T leaves the station at 10am. Twenty minutes later, Train G leaves the same station heading in the same direction as Train T. Train T travels at 50mph while Train G travels

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: Train T leaves the station at 10am. Twenty minutes later, Train G leaves the same station heading in the same direction as Train T. Train T travels at 50mph while Train G travels      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1035059: Train T leaves the station at 10am. Twenty minutes later, Train G leaves the same station heading in the same direction as Train T. Train T travels at 50mph while Train G travels at 60mph.
How long, what time and how far are the trains from the station when Train G catches up Train T?
I know d=rt, r=d/t and that t=d/r but I'm truly stuck on this one.
Thank you so much.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39621) About Me  (Show Source):
You can put this solution on YOUR website!
Try putting all values into variables. You already know the travel rates formula. 

TRAIN        RATE        TIME      DISTANCE
T             r          t+h        d
G             R           t         d

system%28r=50%2CR=60%2Ch=1%2F3%29
Solve for t and d.


USE THE TRAVEL RATE FORMULA TO MAKE A SYSTEM OF EQUATIONS.
system%28r%28t%2Bh%29=d%2CRt=d%29

SOLVE FOR t AND d. You should find formulas for each.

Answer by ikleyn(52824) About Me  (Show Source):
You can put this solution on YOUR website!
.
Train T leaves the station at 10 am. Twenty minutes later, Train G leaves the same station heading in the same direction as Train T.
Train T travels at 50 mph while Train G travels at 60 mph.
How long, what time and how far are the trains from the station when Train G catches up Train T?
I know d=rt, r=d/t and that t=d/r but I'm truly stuck on this one.
Thank you so much.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

In 20 minutes after train T started, it will be at the distance %281%2F3%29%2A50 miles from the station.

( 1%2F3 is 1%2F3 of an hour, or 20 minutes! )

Let "t" be the time measured after 10:20 am, when both train are running till the moment when the train G catches up the train T.

During this time "t" the train T covers the distance 50*t miles (so, you use the formula d = rt just in the second time).

During this time "t"the train G covers the distance 60*t miles (so, you use the formula d = rt just in the third time).

But the distance covered during the time "t" by the train G is by the value of %281%2F3%29%2A50 longer than that covered 
by the train T during the same time "t". It gives you an equation

60*t = 50*t + %281%2F3%29%2A50.

To solve it, multiply both side by 3. You will get

180t = 150t + 50,

180t - 150t = 50,

30t = 50, 

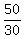t = 50%2F30 = 5%2F3 hour = 100 minutes = 1 hour and 40 minutes.

So, the train G will catch the train T in 1 hour and 40 minutes, counting from 10:20 am. 
In other words, the train G will catch the train T at noon, 12:00. 


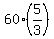During 1 hour and 40 minutes (=5%2F3 hour) the train G will cover 60%2A%285%2F3%29 = 100 miles.

So, the train G will catch the train T in 100 miles from the station.


Did I answered all your questions?

See the lesson Travel and Distance problems in this site and many other lessons on Travel and Distance, associated with it.