.
Please help me simplify the following expression I linked below.
http://postimg.org/image/71l67l0n5/
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The assignment says: simplify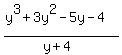 
.
There are several ways to do it.
1. For those who knows what the "Remainder Theorem" is.
The "Remainder Theorem" says (see the lesson Divisibility of polynomial f(x) by binomial x-a in this site):
The binomial 
factors the polynomial 
if and only if
the value of 
is the root of the polynomial , i.e. 
.
In your case the denominator (y+4) makes a hit to you: check if the value (-4) is the root of the polynomial in the numerator.
If you do (it is easy!), you will get that the number (-4) is really a root of that polynomial.
Then, according to the "Remainder Theorem", the binomial (y+4) factors the numerator. It means that the binomial (y+4) divides
the polynomial 
without a remainder, or "with the zero remainder".
Inspired by this observation, you can perform long division and find a quotient. This quotient, which should be a polynomial
of degree 2, will be your answer.
2. But you still can solve it even without knowing about the "Remainder Theorem".
Simply make this long division directly: divide by (y+4). If you do, you get
: 
= 
.
It is your answer.
3. The last, third way, is to factor the polynomial in the numerator using the method of "grouping" instead of making long division:
=
= 
=
= 
=
= 
=
= 
=
= 
.
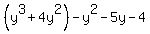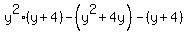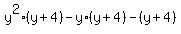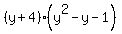Thus the quotient is 
.
It is your answer.
This last, third, way is for those who don't know what the long division is, or don't want to apply it.
(