|
Question 1034806: The Wooden Toy Company makes puzzles and blocks. Each set of blocks takes 30 minutes to cut and 20 minutes to paint. Each puzzle takes 10 minutes to cut and 30 minutes to paint. In a given day, the company has 12 hours of employee time available for cutting and 15 hours available for painting. The company makes a profit of $6.00 on each puzzle and $4.50 on each set of blocks.
A. Let b = the number of sets of blocks and p = the number of puzzles the company makes in a given day. Translate the constraints into a system of linear inequalities.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let b = the number of blocks produced.
let p = the number of puzzles produced.
your constraints are:
b >= 0
p >= 0
this is because the number of blocks and the number of puzzles can't be negative.
30b + 10p <= 720
20b + 30p <= 900
you have to translate everything to the same measure.
you can convert everything to minutes or you can convert everything to hours or you can convert everything to days, but .....
they all have to be in the same quantity of measure.
i chose minutes.
12 hours * 60 minutes per hour = 720 minutes
15 hours * 60 minutes per hour = 900 minutes
the first equation above says that 30 minutes * number of blocks plus 10 minutes * number of puzzles has to be less than or equal to total cutting time of 720 minutes.
the second equation above says that 20 minutes * number of blocks 30 minutes * number of puzzles has to be less than or equal to total painting time of 900 minutes.
those are your constraints.
your objective function is 4.5b + 6p.
this is what you want to maximize.
the above is what you need to solve your problem.
anything further is just extra to show what you do with this information once you have it.
the main idea is to graph the constraints and find the corner points of the feasible region and then to evaluate the objective function at each of the corner points to find out which corner point give you the maximum profit.
what you do is you graph the equality portion of the inequalities and then you shade the area of the graph that satisfies the inequality portion of the equations.
you also need to convert b to x and p to y because most graphing software requires you use x and y variables.
you only have to do this is you are generating the graph using software.
if you are generating the graph manually, you can call the horizontal and vertical axes whatever you want.
a word about an inequality.
if the sign is = only, then it is an equation.
if the sign is >, <, >=, <=, then it is an inequality.
the equality portion of the inequality is the equal sign part.
for example, the equality portion of the inequality of x >= 0 would be the equation x = 0.
a word about graphing software.
most graphing software requires you to put your equations in the form of y = an expression involving x variable and constants.
desmos.com graphing software doesn't.
with desmos, you can enter 30x + 10y = 720
with most other graphing software, you would need to solve the equation for y in terms of x and then enter the equation in the form of y = an expression involving x and a constant.
30x + 10y = 720 would translate to y = (720 - 20x) / 10.
you would need to graph that using most other software.
i used desmos, so i used the first form as you will see when you view the graph.
but, back to the story.....
you graph the constraints and you evaluate the objective function at each of the corner points.
what i usually do is generate the graph using software and then print the graph and then manually make adjustments that aren't easy to do using the software and then scan the graph back into the computer and upload it to my website so you can view it when you are looking as my solution to the problem.
my graph is shown below:
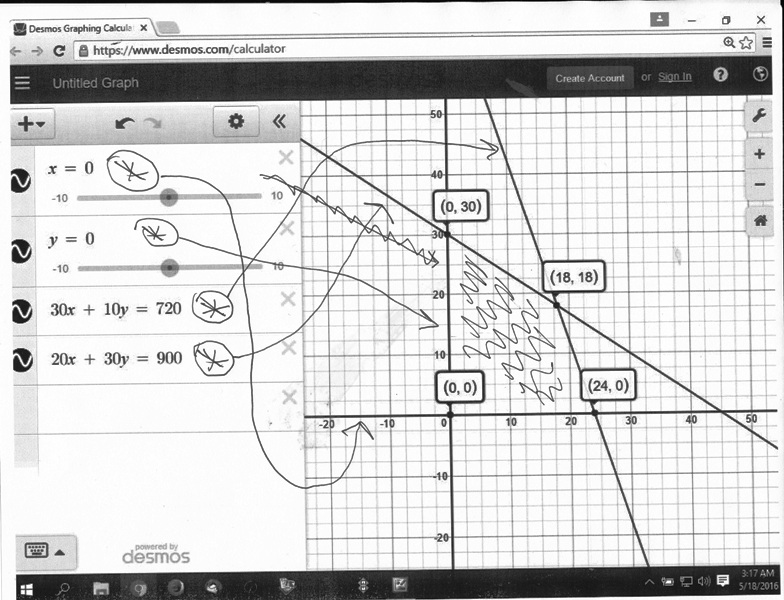
i had the software generate the lines.
i pointed from the equations to the lines that they generated so you can see which lines were generated by which equations.
i had the software show the intersection at the corner points.
desmos was able to generate all lines.
other graphing software would probably not be able to generate x = 0, so you would have to do that by hand if you wanted to make it stand out.
the shaded region shown is to the right of the y-axis and above the x-axis and below the line of 30x + 10y = 720 and below the line of 20x +30y = 900.
that shaded region satisfies all the inequalities at the same time.
the objective function is evaluated at each corner point.
for example when the corner point is (18,18), that means the value of x is 18 and the value of y is 18.
x in the graph means number of blocks which started out as your b variable.
y in the graph means number of puzzles which stated out as your p variable.
the objective function is 4.5x + 6y.
18 * 4.5 + 18 * 6 = a profit of 189.
that was the maximum profit that you will find if you analyze each of the other corner points the same way.
you also need to evaluate the constraints to see if they agree with what is shown on the graph.
18 * 30 + 18 * 10 = 720 minutes of cutting time so this constraint of <= 720 of cutting time is satisfied.
18 * 20 + 18 * 30 = 900 minutes of painting time so this constraint of <= 900 minutes of painting time is satisfied.
that would be the solution to this problem because the profit is maximized and the constraints are satisfied.
it just so happens that the maximum profit was attained with maximum utilization of the constraint.
that isn't always the case.
it all depends on the values in the equations.
if the profit on the blocks was much greater than the profit on the puzzles, you might have seen the maximum profit generated by doing all blocks and no puzzles.
in that case, the corner point of (24,0) might have shown the maximum profit while all the constraint were not fully utilized.
|
|
|
| |