Question 1034396: 1. Sketch the graph of the polynomial function f(x) = ‒x4 + 5x3 + 9x2 ‒ 45x in the interval [‒4, 6].
1) Write the polynomial function in factored form.
2) Sketch the graph of the polynomial function, labeling key points on the graph.
3) Describe the characteristics of the graph including: zeros, y-intercept, relative maximum and minimum and end behavior.
(3 points)
2. Sketch the graph of the polynomial function f(x) = ‒x3 ‒ 4x2 + 4x + 16 in the interval [‒5, 3].
1) Write the polynomial function in factored form.
2) Sketch the graph of the polynomial function, labeling key points on the graph.
3) Describe the characteristics of the graph including: zeros, y-intercept, relative maximum and minimum and end behavior.
(3 points)
.
3. Use what you have learned about the Remainder Theorem to show that X +1 is a factor of 19x42 + 18x -1.
(3 points)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.  in the interval in the interval 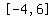 . .
1) Notice that two "parts" of the polynomial share 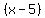 as a common factor: as a common factor:
 and and  , ,
then factor by parts.

Alternatively, youu could take  , or , or  out as a common factor for the whole polynomial first: out as a common factor for the whole polynomial first:

2) and 3) Each teacher/ instructor may have slightly different expectations about how to "sketch the graph of the polynomial function, labeling key points on the graph", but the calculations needed for the sketch would involve finding the values of  for the zeros, minima, and maxima, and figuring out the end behavior of the function. for the zeros, minima, and maxima, and figuring out the end behavior of the function.
The y-intercept is easy:
For  , the value of the function is , the value of the function is  , ,
so we can say that the y-intercept is  . .
We know that the point 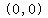 , the origin, is part of the graph of the function, and that will be the first point we plot in our sketch. , the origin, is part of the graph of the function, and that will be the first point we plot in our sketch.
The "end behavior" we are concerned with for the sketch in the interval 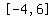 is what happens at is what happens at  and and  . .
Since  , ,
 and and
 . .
In general, the end behavior of a function involves limits,
but in the case of polynomials,
we learned early in algebra that the end behavior is determined by
the leading coefficient (whether it is positive or negative), and
the degree of the polynomial (whether it is even or odd).
A polynomial's end behavior is the same as the end behavior of its first term,
so  behaves as behaves as 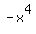 at the ends of the graph: at the ends of the graph:  . .
(The polynomial is negative at both  ends, and ends, and
as we go towards those ends, the polynomial's absolute value increases without bounds).
The zeros are obvious from the factored form of the polynomial,  . .
 for the values of for the values of  that make it factor zero, that make it factor zero,
 , ,  , ,  , and , and  . .
At each one of those zeros, the factor involved changes sign, and so does the function, so
 for for  , ,
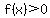 for for 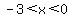 , ,
 for for 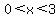 , ,
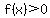 for for 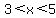 , and , and
 for for  . .
That is useful information for your sketch,
and would lead you to conclude that the polynomial must have
a relative maximum in the interval 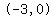 , for , for 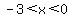 , ,
a relative minimum in the interval  , for , for 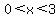 , and , and
a relative maximum in the interval 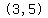 , for , for 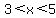 . .
To locate those relative maxima and minimum,
we need the derivative, and we need to calculate the zeros of the derivative.
The derivative is  . .
That polynomial cannot be factored, but it must change signs at least once,
because its degree is  , which is an odd number. , which is an odd number.
In fact, it is not hard to see that it changes signs  times, because times, because
for   , ,
for   , ,
for   , and , and
for   . .
So it must have  zeros, but those zeros must be irrational numbers, zeros, but those zeros must be irrational numbers,
because we cannot factor it.
We cannot find any rational zeros of the form  where where
 is a factor of the leading coefficient is a factor of the leading coefficient  , and , and
 is a factor of the independent term is a factor of the independent term  . .
All we can do is use a calculator to find that the zeros of derivative.
A graphing calculator (if we know how to use it) would make it easier,
but with any calculator (or a spreadsheet) we can try values to "zero in" on those zeros,
and find that the zeros of derivative
 are approximately are approximately
 , ,  , and , and  . .
We can use the calculator to find the value of  at those points as approximately at those points as approximately 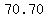 , , 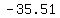 , and , and 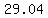 . .
That tells you to include the points
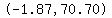 , , 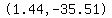 , and , and 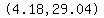 in the sketch. in the sketch.
So far, you have 8 points of your sketch:

For a sketch, all you have to do is join those points with a smooth curve, like this:
 . .
2.  in the interval in the interval 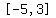 . .
1) The rational zero theorem tells us that a rational zero of that polynomial must be of the form  , where , where
 is a factor of the leading coefficient is a factor of the leading coefficient  , and , and
 is a factor of the independent term is a factor of the independent term  . .
The choices are -16, -8, -4, -4, -2, -1, 1, 2, 4, 8, and 16.
Trying them , starting with the easy ones, we find that  and and  are not zeros. are not zeros.
However,  is a zero, and dividing the polynomial by is a zero, and dividing the polynomial by 
we get  , ,
whose zeros are  , and , and  . .
So,  . .
 --> -->
2) and 3) Two points we need to include in the sketch are
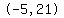 for for  , and , and
 for for  . .
Other points for the sketch are zeros, y-intercept, minimum and maximum.
The zeros of the function are  , ,  , and , and  . .
Those zeros mark points 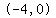 , , 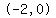 and and 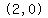 , ,
also to be included in the sketch of the graph.
The y-intercept is  , ,
which tells you that 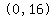 is one point on the graph. is one point on the graph.
The maxima and minima are zeros of derivative
 . .
Those zeros are the solutions to  : :
 or approximately or approximately  and and  . .
The minimum and maximum of the function are
approximately  and and respectively. respectively.
So, points  and and  , ,
also need to be included in the sketch of the graph.
The sketch would look something like this:
 . .
3) According to the Remainder Theorem,
the remainder of the division of 
by  is is 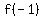 . .
Since that remainder is zero:
 , ,
and that means that  is divisible by is divisible by 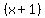 , ,
or in other words that  is a factor of is a factor of  . .
|
|
|