Question 1034287: 1. A polynomial function is shown below.
f(x) = x^6 + 12x^5 + 43x^4 + 22x^3 - 138x^2 - 280x -200
a. Find the real zeros of f (x).
b. Express f (x) in terms of linear factors.
c. Find all of the zeros of f (x).
(3 points)
''.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Rational Roots Theorem with synthetic division indicate possible zeros to check are the positive and negative
of 1,2,4,5,8,10,25,50,100. A graphing tool might help to decide which of the possibilities to try first.
Here are some of the productive synthetic-division root checkings. The first dividend of coefficients to start is
1 12 43 22 -138 -280 -200 ; the roots being checked are shown to the left, in the "divisor" location.
-2 | 1 12 43 22 -138 -280 -200
|
| -2 -20 -46 48 180 200
|____________________________________________________
1 10 23 -24 -90 -100 0
-5 | 1 10 23 -24 -90 -100
|
| -5 -25 10 70 100
|____________________________________________________
1 5 -2 -14 -20 0
-5 | 1 5 -2 -14 -20
|
| -5 0 10 20
|____________________________________
1 0 -2 -4 0
2 | 1 0 -2 -4
|
| 2 4 4
|______________________________
1 2 2 0
This last quotient, having remainder 0, indicates the polynomial factor 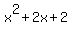
and the zeros are found using general solution formula of a quadratic equation.
Zeros are 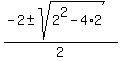
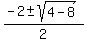
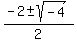
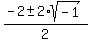
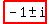
---------------------------------------------------------
To summarize all of these zeros-finding results,
REAL RATIONAL ZEROS:
-5 of multiplicity two;
-2
+2
COMPLEX ZEROS:
-1-i and -1+i
----------------------------------------------------------
To begin in forming the factorized form of your function, start with this, and then simplify the complex part if you want.

Answer by ikleyn(52786)   (Show Source): (Show Source):
|
|
|