Question 1034271: A collection of nickels, dimes, and quarters consist of 60 coins with a total of $6.50. If there are 3 times as many dimes as quarters, find the number of each type of coins.
Found 3 solutions by addingup, ikleyn, MathTherapy:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! n+d+q = 60
d = 3q
0.05n+0.10d+0.25q = 6.50
0.05n+0.10(3q)+0.25q = 6.50
0.05n+0.30q+0.25q = 6.50
0.55q = 6.50-0.05n This is how far I can go with the information you provided
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A collection of nickels, dimes, and quarters consist of 60 coins with a total of $6.50.
If there are 3 times as many dimes as quarters, find the number of each type of coins.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
From the condition, you have these tree equations for three unknowns
n + d + q = 60, (1)
d = 3q, (2)
5n + 10d + 25q = 650. (3)
Since you have 3 independent equations for three unknowns, it is enough to get the solution.
Substitute d = 3q from the equation (2) first into equation (1) and then into equation (3).
In this way you exclude the unknown d and will get the system of TWO equations in TWO unknowns
n + 3q + q = 60, (1')
5n + 10*(3q) + 25q = 650. (2')
or simplifying,
n + 4q = 60, (1'')
5n + 55q = 650. (2'')
To solve this system, let's do one more step of the substitution method.
Express n = 60 - 4q from (1'') and substitute it into equation (2''). You will get
5*(60-4q) + 55q = 650.
Simplify and solve it for q:
300 - 20q + 55q = 650,
35q = 650 - 300,
35q = 350,
q = 10.
Congratulations! You just found the number of quarters.
Now you can find the number of nickels.
Use the formula n = 60 - 4q that you obtained above. You will get
n = 60 - 4*10 = 60 - 40 = 20. So, the number of nickels is 20.
Last step is to find the number of dimes. For it, use the formula d= 3q (equation (2)). You have d = 3*10 = 30.
Answer. n = 20, d = 30, q = 10.
Please check yourself that the solution is correct.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A collection of nickels, dimes, and quarters consist of 60 coins with a total of $6.50. If there are 3 times as many dimes as quarters, find the number of each type of coins.
Let number of nickels and quarters, N, and Q, respectively
Then number of dimes = 3Q
We then get: N + Q + 3Q = 60_____N + 4Q = 60 ------- eq (i)
Also, .05N + .25Q + .1(3Q) = 6.5____.05N + .25Q + .3Q = 6.5____.05N + .55Q = 6.5 ---- eq (ii)
- .05N - .2Q = - 3 ------- Multiplying eq (i) by – .05 ------- eq (iii)
.35Q = 3.5 ------- Adding eqs (iii) & (ii)
Q, or number of quarters = 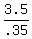 , or , or 
N + 4(10) = 60 --------- Substituting 10 for Q in eq (i)
N + 40 = 60
N, or number of nickels = 60 – 40, or 
Number of dimes: 3(10), or 
|
|
|