SOLUTION: i know i^2 =-1 so i^26 must be -1. but i can write i^26 as (i^4)^(26/4) and we know i^4 is 1 so it is 1. my question is what is my mistake here? and can i write (i)3/2 as (

Fractional exponents must be avoided in mathematics courses 
less advanced than complex analysis.  In complex analysis 
there are "multi-valued functions".

There are two square roots of, say, 4, +2 and -2.
However, in math courses less advanced than complex analysis,
we restrict the symbol  to mean only the positive
square root of 4, not -2.  If we want the other square root,
-2, we must write 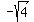.  That agreement was made 
so that the square root relation would be a function, passing 
the vertical line test.

But imaginary (complex) numbers are neither positive nor 
negative, so no such agreement is possible.  +i is neither a 
positive number nor a negative number. Likewise -i is neither
a negative number nor a positive number. 

So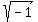  

and its equivalent expression 



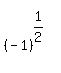actually is double valued and means both the values,



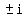but that is in the more advanced course complex analysis.

Until we study the advanced mathematics course of complex
analysis, we must avoid writing radicals or fraction
exponents of negative or imaginary numbers.

Therefore 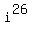 may not be written as 



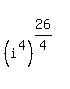in lower math courses because it involves a fractional 
exponent of an imaginary number.

Edwin