Question 1034158: Show that a line through the origin of R^3 is a subspace of R^3
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let L be any line in  that passes through the origin. Then it would have the symmetric equation that passes through the origin. Then it would have the symmetric equation  with as its direction vector. with as its direction vector.
Let w and v be two vectors in L. Then w = k(a,b,c) and v = l(a,b,c) for some constants k and l.
Now a non-empty subset of any vector space is a subspace iff 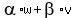 is also in the subset for any two vectors w and v in the said subset. is also in the subset for any two vectors w and v in the said subset.
But 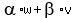 = =  *k(a,b,c) + *k(a,b,c) +  *l(a,b,c) *l(a,b,c)
= ( *k + *k +  *l)(a,b,c), *l)(a,b,c),
meaning the resulting linear combination is still in the line L.
Hence any line through the origin of  is a subspace of is a subspace of 
|
|
|