Question 1034091: find the equation of the tangent and normal of the curve x^2-2y^2+4=0, perpendicular to 2x-y+7=0
Found 2 solutions by macston, ikleyn:
Answer by macston(5194)   (Show Source):
You can put this solution on YOUR website! .
Strictly speaking, this is not an algebra question. If you are studying calculus,it is possible to figure this. If you want an algebraic solution, it will be several pages, and I will provide it one page at a time, asking you to respond after each page, so I know the effort is worth it. If you want a calculus solution I will post it shortly to this question. If you do not respond, I will assume calculus and post within 24 hours. Algebra answers to calculus questions require a lot of time.
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
find the equation of the tangent and normal of the curve x^2-2y^2+4=0, perpendicular to 2x-y+7=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You, probably, know how to write an equation of the straight line perpendicular to 2x-y+7 = 0.
It is 2y+x+c = 0. It is the entire family of parallel lines depending on the coefficient "c".
Now, to get the tangent line to the given hyperbola, you need to find the coefficient "c" ("the line") from the system
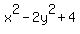 =  (1)
x + 2y + c = 0 (2)
under the condition that the system has one and only one solution.
In this way you will get the tangent line.
How to solve the system (1), (2)?
Very simple. Express x from (2) and substitute it into (1).
You will get a single quadratic equation for y.
The condition that it has one and only one real solution is vanishing its discriminant d = 0.
So, express that "d" via "c" and find "c" as a root of the equation d = 0.
For inspiration, see the lesson
Tangent lines and normal vectors to a hyperbola.
By the way, the curve x^2-2y^2+4=0 is a hyperbola.
Good luck!
|
|
|
