Question 1034075: Jane wants to buy a photocopier. The sales person has the following information on three models. If all three are used, a specific job can be completed in 50 minutes. If copier A operates for 20 minutes and copier B operates for 50 minutes, then one-half the job can be is completed. If copier B operates for 30 minutes and copier C operates for 80 minutes, then three-fifths of the job can be completed. Which is the fastest copier, and how long does it take for this copier to complete the entire job?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52886)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jane wants to buy a photocopier. The sales person has the following information on three models.
If all three are used, a specific job can be completed in 50 minutes.
If copier A operates for 20 minutes and copier B operates for 50 minutes, then one-half the job can be is completed.
If copier B operates for 30 minutes and copier C operates for 80 minutes, then three-fifths of the job can be completed.
Which is the fastest copier, and how long does it take for this copier to complete the entire job?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x = rate of work of the copier A in units  ;
y = rate of work of the copier B -------- " -----------;
z = rate of work of the copier C -------- " -----------.
So, my x = 1/a, my y = 1/b and my z = 1/c of the other tutor.
As the condition says, if all three copiers work, the job is done in 50 minutes: 50x + 50y + 50z = 1.
If copier A operates for 20 minutes and copier B operates for 50 minutes, then one-half the job can be is completed.
It means 20x + 50y = ;
y = rate of work of the copier B -------- " -----------;
z = rate of work of the copier C -------- " -----------.
So, my x = 1/a, my y = 1/b and my z = 1/c of the other tutor.
As the condition says, if all three copiers work, the job is done in 50 minutes: 50x + 50y + 50z = 1.
If copier A operates for 20 minutes and copier B operates for 50 minutes, then one-half the job can be is completed.
It means 20x + 50y =  .
If copier B operates for 30 minutes and copier C operates for 80 minutes, then three-fifths of the job can be completed.
It means 30y + 80z = .
If copier B operates for 30 minutes and copier C operates for 80 minutes, then three-fifths of the job can be completed.
It means 30y + 80z =  .
So you have three equations for three unknowns:
50x + 50y + 50z = 1, (1)
20x + 50y = .
So you have three equations for three unknowns:
50x + 50y + 50z = 1, (1)
20x + 50y =  , (2)
30y + 80z = , (2)
30y + 80z =  . (3)
Notice, this system is LINEAR !!!!!
Now, to solve it, I will do this TRICK.
1. Add equations (2) and (3) (both sides). You will get
20x + 80y + 80z = . (3)
Notice, this system is LINEAR !!!!!
Now, to solve it, I will do this TRICK.
1. Add equations (2) and (3) (both sides). You will get
20x + 80y + 80z =  . (4) ( <--- . (4) ( <--- 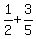 = =  ).
2. Multiply equation (1) by 8, multiply equation (4) by 5 and write them one under the other, like this:
400x + 400y + 400z = 8, (5)
100x + 400y + 400z = ).
2. Multiply equation (1) by 8, multiply equation (4) by 5 and write them one under the other, like this:
400x + 400y + 400z = 8, (5)
100x + 400y + 400z =  . (6)
3. What to do next? But of course, distract (6) from (5). You will get
300x = 8 - . (6)
3. What to do next? But of course, distract (6) from (5). You will get
300x = 8 -  = =  = =  .
Hence, x = .
Hence, x =  = =  . It is the rate of work of the copier A.
Almost all is done. Now from equation (2) you can easily find "y" and from equation (3) find "z".
Please complete these calculations and complete the solution on your own. . It is the rate of work of the copier A.
Almost all is done. Now from equation (2) you can easily find "y" and from equation (3) find "z".
Please complete these calculations and complete the solution on your own.
By the way, the nonlinear system of the other tutor also can be solved as a LINEAR after substitution x = 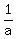 , y = , y =  and z = and z = 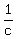 by the same way. by the same way.
I just explained this TRICK in my lesson Solving systems of non-linear equations in three unknowns using Cramer's rule in this site.
See also the lesson Joint-work problems for 3 participants.
The lesson you should learn from this solution is this:
When solving a non-standard joint-work problem, double think which variable to choose as an unknown: the-time-to-complete-the-job OR the rate-of-work.
|
|
|