Question 1033906: At football games last year, the snack shop took in $1200 in soft drink sales. This year the price per drink was raised 15 cents, 300 fewer drinks were sold, and $1365 was brought in. Find the price of the soft drinks and the numbers sold
Found 2 solutions by algebrapro18, MathTherapy:
Answer by algebrapro18(249)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! At football games last year, the snack shop took in $1200 in soft drink sales. This year the price per drink was raised 15 cents, 300 fewer drinks were sold, and $1365 was brought in. Find the price of the soft drinks and the numbers sold
Let price, per drink, last year be P
Then number sold last year = 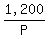
Increasing price by .15, this year, makes the new price, P + .15
Since 300 fewer were sold this year, then number sold this year = 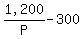
We then get: 
 ------- FOILing left side ------- FOILing left side

 ------- Multiplying by LCD, P ------- Multiplying by LCD, P


 ------- Factoring out GCF, 30 ------- Factoring out GCF, 30
(2P – 1)(5P + 6) = 0 ------- Factoring the above trinomial
2P – 1 = 0 OR 5P + 6 = 0 (ignore)
2P = 1
P, or price last year = ½, or $0.50
Price this year: $0.50 + .15 = 
Number sold this year: 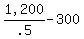 , or 2,400 – 300, or , or 2,400 – 300, or 
|
|
|