Question 1033806: Please help me with this problem:
Let f be the function f(x) = 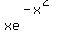 where x is a set of real numbers. Find the critical numbers of f. (It is helpful to note that where x is a set of real numbers. Find the critical numbers of f. (It is helpful to note that 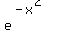 is nonzero for any value of x.) Find the intervals on which f is increasing and on which f is decreasing. Use the information found to tell where f attains local maximum and minimum values. is nonzero for any value of x.) Find the intervals on which f is increasing and on which f is decreasing. Use the information found to tell where f attains local maximum and minimum values.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ==> f'(x) = ==> f'(x) = 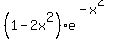 . .
Let f'(x) be equal to 0.
==>  ==> ==>  or or  , the critical numbers of f(x). , the critical numbers of f(x).
As you mentioned 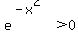 , so no solution comes from this. , so no solution comes from this.
In ( , ,  ), f'(x) < 0, so f(x) is decreasing there. ), f'(x) < 0, so f(x) is decreasing there.
In ( , , ), f'(x) > 0, so f(x) is increasing there. ), f'(x) > 0, so f(x) is increasing there.
In ( , , ), f'(x) < 0, so f(x) is decreasing there. ), f'(x) < 0, so f(x) is decreasing there.
Therefore f(x) attains local min at  , while it attains a local max at , while it attains a local max at  . .
|
|
|