Question 1033703: Convert the polar equation to cartesian/rectangular coordinates
(r^2) cos (2 theta) = 2
Thank you!
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Convert the polar equation to cartesian/rectangular coordinates
(r^2) cos (2 theta) = 2
------
Note: The polar form is r(cos(t)+i(sin(t)))
-----------------------
I don't recognize your equation::
------------
Cheers,
Stan H.
-------------
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Convert the polar equation to cartesian/rectangular coordinates
(r^2) cos (2 theta) = 2
Thank you!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's do it together.
We start with the point (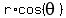 , , ) in a coordinate plane. This point is presented in the polar form,
and we want to learn what is a curve ) in a coordinate plane. This point is presented in the polar form,
and we want to learn what is a curve 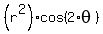 = =  .
Do you know that .
Do you know that 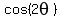 = = 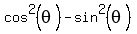 ?
It is the direct consequence of the addition formula for cosine.
Also, it is named the formula for double argument for cosine.
If you don't know it, then look in these lessons
Addition and subtraction formulas
Trigonometric functions of multiply argument
OK. Having this, let's make one step further. ?
It is the direct consequence of the addition formula for cosine.
Also, it is named the formula for double argument for cosine.
If you don't know it, then look in these lessons
Addition and subtraction formulas
Trigonometric functions of multiply argument
OK. Having this, let's make one step further.
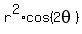 = = 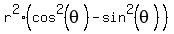 = = 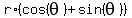 . .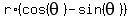 = = 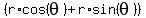 . .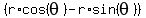 . (1)
Now, . (1)
Now, 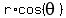 is x-component of the point ( is x-component of the point (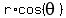 , ,  ) in the rectangular coordinate system on the coordinate plane.
So we can write ) in the rectangular coordinate system on the coordinate plane.
So we can write  = = 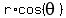 .
Similarly, .
Similarly,  is y-component of the point ( is y-component of the point (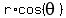 , , ) in the rectangular coordinate system on the coordinate plane.
So we can write ) in the rectangular coordinate system on the coordinate plane.
So we can write  = =  .
Therefore, we can rewrite the formula (1) in this way: .
Therefore, we can rewrite the formula (1) in this way:
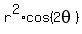 = = 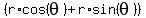 . .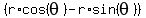 = = 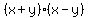 = =  . (3)
Then your original equation . (3)
Then your original equation 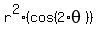 = =  becomes becomes
 = =  .
Do you recognize this equation ? What is this ? Is it familiar to you ?
But of course, it is the equation of a hyperbola . . .
So, we unraveled this mystery. .
Do you recognize this equation ? What is this ? Is it familiar to you ?
But of course, it is the equation of a hyperbola . . .
So, we unraveled this mystery.
-------------------------------
Comment from student: It looks like the equation for a circle to me. A circle with a diameter of 2 centered at (0,0), correct? Thank you for your help!
-------------------------------
My response: Do not make a mistake !
It is definitely the equation of a HYPERBOLA.
About equations for hyperbola see the lesson Hyperbola definition, canonical equation, characteristic points and elements in this site.
|
|
|