SOLUTION: if there are at least one of each type of coin, and there are 28 coins in total, what possible combinations of nickles, dimes, and quarters will add up to 2 dollars using matricies

Algebra ->  Customizable Word Problem Solvers  -> Coins -> SOLUTION: if there are at least one of each type of coin, and there are 28 coins in total, what possible combinations of nickles, dimes, and quarters will add up to 2 dollars using matricies      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1033597: if there are at least one of each type of coin, and there are 28 coins in total, what possible combinations of nickles, dimes, and quarters will add up to 2 dollars using matricies
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Let n = number of nickels, d = number of dimes, and q = number of quarters.
We have to solve the system
n+d+q = 28
0.05n+0.10d+0.25q = 2.00
The second equation is equivalent to n + 2d + 5q = 40, after simplification.
The system represented as an augmented matrix is
%28matrix%282%2C4%2C1%2C1%2C1%2C28%2C1%2C2%2C5%2C40%29%29
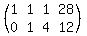~%28matrix%282%2C4%2C1%2C1%2C1%2C28%2C0%2C1%2C4%2C12%29%29 ~ %28matrix%282%2C4%2C1%2C0%2C-3%2C16%2C0%2C1%2C4%2C12%29%29
==> n-3q = 16 and d+4q = 12.
==> n = 3q+16 and d = 12 - 4q.
==> The possible values of q are 0,1, 2, and 3.
The possible triples (n,d,q) are thus
(16,12,0), (19,8,1), (22,4,2), and (25,0,3).
But since there is at least one of each type of coin, the only possible combinations are (19,8,1) and (22,4,2).