Question 1033540: TRIANGLE ABC and TRIANGLE XYZ are similar triangles. If BA = x + 7, AC = x + 4, YX = x + 2, and XZ = x + 3, find the value of x.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
TRIANGLE ABC and TRIANGLE XYZ are similar triangles. If BA = x + 7, AC = x + 4, YX = x + 2, and XZ = x + 3, find the value of x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since triangles ABC and XYZ are similar, their corresponding sides (side dimensions) are proportional.
In particular,
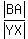 = = 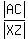 , or , or  = = 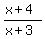 . (1)
To find "x", cross-multiply. You will get
(x+7)*(x+3) = (x+2)*(x+4).
Simplify and solve for x: . (1)
To find "x", cross-multiply. You will get
(x+7)*(x+3) = (x+2)*(x+4).
Simplify and solve for x:
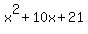 = = 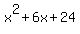 , or
4x = 3,
x = , or
4x = 3,
x =  . .
|
|
|