Question 1033415: Let x, y, and z be nonzero real numbers. Find all possible values of
(x)/(|x|) + (y)/(|y|) + (z)/(|z|) + (xyz)/(|xyz|).
List your values in increasing order, separated by commas.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52792)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x, y, and z be nonzero real numbers. Find all possible values of
(x)/(|x|) + (y)/(|y|) + (z)/(|z|) + (xyz)/(|xyz|).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let F(x,y,z) = 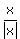 + + 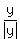 + + 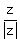 + + 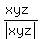 .
It is clear that it is sufficient to estimate/calculate F(x,y,z) at x = +/-1, y = +/-1 and z = +/-1. In total, there are 8 inputs.
If there are all "+" in the input, the result is 4.
If there is precisely 1 "-" in the input, then the result is 0.
If there are precisely 2 "-" in the input, then the result is 0.
If there are all "-" in the input, then the result is -4.
Answer. The list of all possible values is 4, 0, -4. .
It is clear that it is sufficient to estimate/calculate F(x,y,z) at x = +/-1, y = +/-1 and z = +/-1. In total, there are 8 inputs.
If there are all "+" in the input, the result is 4.
If there is precisely 1 "-" in the input, then the result is 0.
If there are precisely 2 "-" in the input, then the result is 0.
If there are all "-" in the input, then the result is -4.
Answer. The list of all possible values is 4, 0, -4.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Case 1. All three variables positive: x>0, y>0, z>0
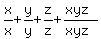
   Case 2. Two of the variables positive, one negative
By symmetry, it doesn't matter which one is negative,
the answer will be the same. Say, only y is negative:
x>0, y<0, z>0
Case 2. Two of the variables positive, one negative
By symmetry, it doesn't matter which one is negative,
the answer will be the same. Say, only y is negative:
x>0, y<0, z>0

   Case 3. One of the variables positive, two negative
Also by symmetry, it doesn't matter which one is positive,
the answer will be the same. Say, only x is positive
x>0, y<0, z<0
Case 3. One of the variables positive, two negative
Also by symmetry, it doesn't matter which one is positive,
the answer will be the same. Say, only x is positive
x>0, y<0, z<0
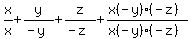
   Case 4. All three negative: x<0, y<0, z<0
Case 4. All three negative: x<0, y<0, z<0
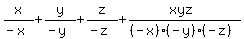
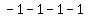   In increasing order, separated by commas:
-4,0,4
Edwin
In increasing order, separated by commas:
-4,0,4
Edwin
|
|
|