Question 1033395: Given a parallelogram ABCD and and a line l outside the parallelogram. Let the distance from points A,B,C,D to line l be a,b,c,D respectively. Prove that a+c = b+d
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since in the Euclidean system, (absolute) distance between objects is invariant under translation/rotation/reflection of axes, we can assume that the line L in the problem is the x-axis and the parallelogram lies above the x-axis. (If L is parallel to the x-axis, just translate the latter upward or downward; if L intersects the x-axis at point P, rotate the x-axis around the point P to correspond to line L; if the parallelogram is below the line L, reflect the former so that it is above the line L.)
Now let the leftmost vertex be A(a,b). Then point B (assuming clockwise direction) will be (a + r, 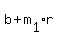 ), where r is any positive real number and ), where r is any positive real number and 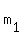 is the slope of the line from point A to B. is the slope of the line from point A to B.
Point D will have coordinates (a+s,  ), where s again any arbitrary positive real number, while ), where s again any arbitrary positive real number, while  is the slope of the line from point A to point D. is the slope of the line from point A to point D.
Finally point C will have coordinates (a+r+s, 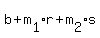 ). The line AB, which has slope ). The line AB, which has slope 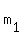 , will then have the same slope as line DC. , will then have the same slope as line DC.
Now the distance of point A from the x-axis is b.
The distance of point B from the x-axis is 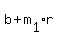 . .
The distance of point C from the x-axis is 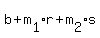 . .
The distance of point D from the x-axis is  . .
==> a+c =  . .
and b + d = 
AND the result immediately follows.
|
|
|