Question 1033358: Write the standard form of the equation for the circle that passes through the points (-2, 30), (-19, -1), and (12, -18). Then identify the center and the radius.
A.(x - 6)² + (y - 5)² = 625; center (6, 5); r = 25
B.(x + 5)² + (y + 6)² = 625; center (5, 6); r = 25
C.(x - 5)² + (y - 6)² = 625; center (5, 6); r = 25
D.(x + 6)² + (y + 5)² = 625; center (6, 5); r = 25
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! After trying this twice on paper, I do not find any of those choices. I am finding the y-coordinate of the center to be 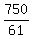 . This does not fit with 5, or -5, or 6, or -6.
I can scan the image of my work and send through email to you.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Write the standard form of the equation for the circle that passes through the points (-2, 30), (-19, -1), and (12, -18). Then identify the center and the radius.
A.(x - 6)² + (y - 5)² = 625; center (6, 5); r = 25
B.(x + 5)² + (y + 6)² = 625; center (5, 6); r = 25
C.(x - 5)² + (y - 6)² = 625; center (5, 6); r = 25
D.(x + 6)² + (y + 5)² = 625; center (6, 5); r = 25
The following sytem of equations, in 3 unkowns (h, k, r), was derived:
Subtracting eq (ii) from (i) and (iii) from (i) yield the following reduced system, in 2 unknowns:
– 17h – 31k = - 271, and
7h – 24k = - 109
When solved, we find (h, k), or center to be (5, 6)
Using the center and one of the given coordinate points result in a radius of 25, so CHOICE C is the correct response.
|
|
|
