.
A body falls freely from the top of the tower and during last second of the fall, it falls through 25 m. Find the height of tower.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Solution 1
This fact is known very well from Physics, or from Calculus or from . . .
Free falling body falls the distance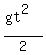 
in t seconds, where "g" is the gravity acceleration.
Therefore, your equation to find the time is
- 
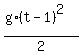= 25.
In this problem, take g = 10 
(actually, g = 9.81 ). You will get
- 
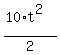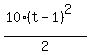= 25, or
= 25, or
= 25, or
10t = 30.
Hence, t = 3 seconds.
For 3 seconds, the body falls = 
= 5*9 = 45 m.
Answer. The height of the building is 45 m.
Solution 2
Calculate the distances the free falling body falls during the 1-st, 2-nd, 3-rd . . . seconds. Use g = 10 .
1-st sec.: 
= 
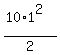= 5 m.
2-nd sec.: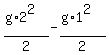 
= 
= 20-5 = 15 m.
3-rd sec.: 
= 
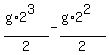= 45-20 = 25 m.
See these numbers: 5, 15, 25 . . .
They form ARITHMETIC PROGRESSION !!!
This remarkable fact is general:
The distances that the free falling body falls during the first second,
the next one, the third and so on, form the arithmetic progression.
Miracle ?! - No, the algebra only. - See the lessons
Free fall and arithmetic progressions
Uniformly accelerated motions and arithmetic progressions
in this site.
And not to forget, the calculations above that lead to the number "25 m in third second" give another solution to the original problem.
