.
2cos^2x + cosx = 0
~~~~~~~~~~~~~~~~~~~~
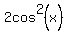 +
+  =
=  , (1)
, (1)
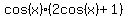 =
=  . (2)
So, our equation (2) deploys in two equations:
1. cosx) = 0 ---> x =
. (2)
So, our equation (2) deploys in two equations:
1. cosx) = 0 ---> x =  , k = 0, +/-1, +/-2, . . . (3)
and
2. 2cos(x) + 1 = 0 ---> cos(x) =
, k = 0, +/-1, +/-2, . . . (3)
and
2. 2cos(x) + 1 = 0 ---> cos(x) =  ---> x =
---> x = 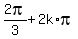 , k = 0, +/-1, +/-2, . . . (4)
and/or x =
, k = 0, +/-1, +/-2, . . . (4)
and/or x =  , k = 0, +/-1, +/-2, . . . (5)
The union of the three sets (3) U (4) U (5) is the set of solutions of the original equation (1).
, k = 0, +/-1, +/-2, . . . (5)
The union of the three sets (3) U (4) U (5) is the set of solutions of the original equation (1).