Question 1033270: Anthony wants to visit the 20 colleges?
Found 2 solutions by KMST, Whiteboy:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! THE FIFTH GRADER'S THOUGHT:
Anthony lets luck of the draw decide.
He writes the name of each college on a small piece of paper, and
puts the pieces of paper in a bag to draw the names at random.
He draws the first piece of paper, and marks it as the first college where he will spend a night.
Of course, he does not put that piece of paper back in the bag, before drawing again to find another college where he will spend a night.
He then draws {"without replacement") a second and a third piece of paper that decide where he will spend the second and third nights respectively.
That decides the schedule of college sleepovers.
There are  possible schedules
(10 possibilities for the first draw, 9 for the second, and 8 for the third draw).
However, each set of  pieces of papers could be drawn in
 orders, and it would still be the same set, just different orders.
There are 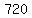 different college sleepover schedules,
but they represent  different sets of sleepover college choices.
The chances that  particular set of colleges could be chosen that way is in  ,
so the probability that Anthony spends a night at Rutgers University, a night at the University of Miami, and a night at Clemson University is
 .
THE MATH TEACHER SAYS:
This is a case of combinations (setof items, where order does not matter).
The number of combinations of  items taken without replacement from a set of  items is
 .
In this case  and  ,
so the number of possible sets of colleges where Anthony could spend the night,
out of the  colleges he wanted to visit is
 .
{Rutgers U, U Miami, Clemson U} is one 3-college subset of the 10-college set of colleges that Anthony wants to visit.
The probability that the set of 3 colleges where Anthony spends a night
is that particular set out of the possible sets is
.
Answer by Whiteboy(6)  (Show Source):
|
|
|
