SOLUTION: Find the point of inflexion on the curve y=xln(x)-x^2. I found the derivative: y'= ln(x+1) -2x But I can't find the point of inflexion because I can't solve for y'=0 Please H

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Find the point of inflexion on the curve y=xln(x)-x^2. I found the derivative: y'= ln(x+1) -2x But I can't find the point of inflexion because I can't solve for y'=0 Please H      Log On


   

Question 1033076: Find the point of inflexion on the
curve y=xln(x)-x^2.
I found the derivative: y'= ln(x+1) -2x
But I can't find the point of inflexion because I can't solve for y'=0
Please Help !!!
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
y=xlnx-x%5E2 ==> y' = lnx + 1 - 2x =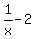=> y" = 1%2Fx-2
The critical values of the 2nd derivative are x = 0 and x = 1/2, but the function y=xlnx-x%5E2 is undefined at x = 0, so there is no inflection point there.
Now in (-infinity, 0), y" < 0.
In (0, 1/2), y" > 0, and
at (1/2, infinity), y" < 0.
(At x = 1/2, y" = 0.)
Hence there is only one inflection point at (1/2, 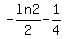-ln2%2F2-1%2F4). (Even though there is a change in the direction of concavity from the interval (-infinity, 0) to (0, 1/2).)