|
Question 1032955: Alec and Beau race to compute 1 + 2 + 3 + ••• + n. Alec skips two numbers and gets a sum of 92. Beau double-counts two numbers and gets a sum of 145. What is the value of n?
Found 3 solutions by Edwin McCravy, rothauserc, AnlytcPhil:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sum of the first n integers is 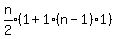 or or 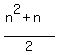 Let the sum of the two integers that Alec skipped be s1.
Let the sum of the two integers that Beau double counted be s2.
Then we have these two equations:
Let the sum of the two integers that Alec skipped be s1.
Let the sum of the two integers that Beau double counted be s2.
Then we have these two equations:
 Subtracting the first equation from the 2nd:
Subtracting the first equation from the 2nd:
 or or  Adding the two equations:
Adding the two equations:
 Substituting
Substituting 
 which simplifies to
which simplifies to
 The discriminant must be a perfect square.
discriminant =
The discriminant must be a perfect square.
discriminant = 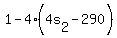 which simplifies to
which simplifies to
 Now we use our TI-83 or TI-84 calculator to
find feasible value(s) of s2 that
will cause
Now we use our TI-83 or TI-84 calculator to
find feasible value(s) of s2 that
will cause  to be a perfect square.
Press the Y= key and put to be a perfect square.
Press the Y= key and put 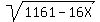 after \Y1
Press 2ND WINDOW (TBLSET) and set TblStart=0 and ΔTbl=1,
highlight the two Auto's
Press 2ND GRAPH (TABLE)
Use the down arrow key to scroll down until you see
an integer in the Y1 column.
The first place we find one is when X=20 and Y1=29
[ We find one again when X=27 and Y1=27, also
when X=45 and Y1=21, X=50 and Y1=19, etc.,
but we will show that these are not possible.]
For now, let's go with the X=20 and Y1=29.
The X on the calculator is our s2.
So if we take s2 = 20
Substituting in after \Y1
Press 2ND WINDOW (TBLSET) and set TblStart=0 and ΔTbl=1,
highlight the two Auto's
Press 2ND GRAPH (TABLE)
Use the down arrow key to scroll down until you see
an integer in the Y1 column.
The first place we find one is when X=20 and Y1=29
[ We find one again when X=27 and Y1=27, also
when X=45 and Y1=21, X=50 and Y1=19, etc.,
but we will show that these are not possible.]
For now, let's go with the X=20 and Y1=29.
The X on the calculator is our s2.
So if we take s2 = 20
Substituting in  , we get , we get  .
Substituting in .
Substituting in  , we get n2+n-210=0
or (n-14)(n+15)=0 and the only solution n=14
So they raced up 14 term:
1+2+3+4+5+6+7+8+9+10+11+12+13+14 = , we get n2+n-210=0
or (n-14)(n+15)=0 and the only solution n=14
So they raced up 14 term:
1+2+3+4+5+6+7+8+9+10+11+12+13+14 = 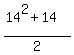 = 105
They would have gotten 105 if they had simply added them all
once each.
Since Alec skipped two integers with sum 13, he only got 105-13 = 92
Since Beau doubled two integers with sum 20, he only got 105+40 = 145.
It would not matter what two integers they skipped or double-counted,
as long as Alec skipped two that had sum 13 and Beau double counted
two that had sum 20.
[We can rule out the other numbers we found on the calculator
since = 105
They would have gotten 105 if they had simply added them all
once each.
Since Alec skipped two integers with sum 13, he only got 105-13 = 92
Since Beau doubled two integers with sum 20, he only got 105+40 = 145.
It would not matter what two integers they skipped or double-counted,
as long as Alec skipped two that had sum 13 and Beau double counted
two that had sum 20.
[We can rule out the other numbers we found on the calculator
since  , , 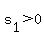 implies implies 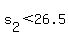 ]
Edwin ]
Edwin
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of n consecutive integers is given by the following formula
:
Sn = n(n+1) / 2
:
therefore
:
92 < n(n+1) / 2 < 145
:
184 < n(n+1) < 290
:
there are two pairs of integers that satisfy this inequality
:
(14, 15) and (15, 16)
:
*************
n is 14 or 15
*************
:
Answer by AnlytcPhil(1807)   (Show Source): (Show Source):
|
|
|
| |