Question 1032587: Triangle. ABC. Area. 100sq metres. Has angles 50 60 & 70. Degrees. Find the. Lengths. Of sides.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Triangle. ABC. Area. 100sq metres. Has angles 50 60 & 70. Degrees. Find the. Lengths. Of sides.
=====================
To solve this, assign a length to 1 of the sides, then find the other 2 using the Law of Sines.
Then find the area of that triangle.
Then use the fact that the area is a function of the square of side length, and find the sides for area = 100 sq meters.
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A triangle ABC has the area of 100 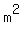 . It has angles of 50°, 60° and 70°. . It has angles of 50°, 60° and 70°.
Find the lengths of the sides of the triangle.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "a", "b" and "c" be the sides of the triangle in a way that the side "a" is opposite to the angle of 60°,
the side "b" is opposite to the angle 50° and the side "c" is opposite to the angle 70°.
We can write these three equality for the area of the triangle:
 = =  , (1) , (1)
 = =  , (2) , (2)
 = =  . (3)
Now, multiply all three equality (1), (2) and (3) (both sides). You will get . (3)
Now, multiply all three equality (1), (2) and (3) (both sides). You will get
 = = 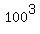 .
It gives .
It gives
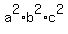 = = 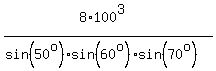 ,
or, after taking the square root from both sides, ,
or, after taking the square root from both sides,
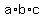 = = 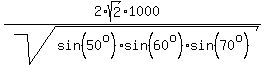 . (4)
Next, let us rewrite the equalities (1) - (3) in the form . (4)
Next, let us rewrite the equalities (1) - (3) in the form
 = =  , (1') , (1')
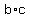 = =  , (2') , (2')
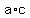 = =  . (3')
We are just at the finish line. Divide (4) by (1'). You will get
c = . (3')
We are just at the finish line. Divide (4) by (1'). You will get
c = 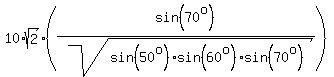 = = 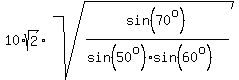 . (5)
Divide (4) by (2'). You will get
a = . (5)
Divide (4) by (2'). You will get
a = 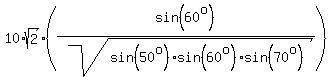 = = 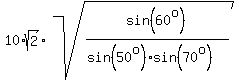 . (6)
Finally, divide (4) by (3'). You will get
b = . (6)
Finally, divide (4) by (3'). You will get
b =  = = 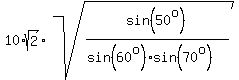 . (7)
Formulas (5), (6) and (7) are the solution of the problem. They allow calculate the sides.
If you want to get numerical values, use sin(50°) = 0.766044, sin(60°) = 0.866025 and sin(70°) = 0.939693. From (5), (6) and (7) you will get
a = 15.5117, b = 13.7209 and c = 16.8312 (approximately). . (7)
Formulas (5), (6) and (7) are the solution of the problem. They allow calculate the sides.
If you want to get numerical values, use sin(50°) = 0.766044, sin(60°) = 0.866025 and sin(70°) = 0.939693. From (5), (6) and (7) you will get
a = 15.5117, b = 13.7209 and c = 16.8312 (approximately).
|
|
|