Question 1032574: As Kyle walked along a street at a constant speed, he noticed that every 12 minutes, a bus passed him traveling in the same direction, and every 4 minutes, a bus passed him traveling in the opposite direction as Kyle. If all of the buses travel at a constant speed and leave the terminals at each end of the street at equally spaced intervals, how many minutes long is that interval?
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As Kyle walked along a street at a constant speed, he noticed that every 12 minutes, a bus passed him traveling in the same
direction, and every 4 minutes, a bus passed him traveling in the opposite direction as Kyle. If all of the buses travel
at a constant speed and leave the terminals at each end of the street at equally spaced intervals, how many minutes
long is that interval?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
0. If all buses travel at a constant speed and leave the terminals at each end of the street at equally spaced intervals,
then the distance between each pair of two consecutive buses is a constant value.
Let L be the distance between any two consecutive bases (measured in meters, for example).
The value L is the same for buses moving in the same direction as Kyle moves.
Also, it is the same value L for all buses moving in opposite direction, as well.
Also, let "u" be the speed of the buses (common for all bases) and "v" be the Kyle's walking speed.
Surely, each speed is relative to the ground, and we use the derived unit 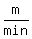 for these speeds.
1. Now, let us consider (imagine) walking Kyle on the street and buses that move opposite to him.
Let us consider the very moment for these speeds.
1. Now, let us consider (imagine) walking Kyle on the street and buses that move opposite to him.
Let us consider the very moment  when one of the buses on the street comes up to the same position as Kyle in his walk-way.
So, at the moment when one of the buses on the street comes up to the same position as Kyle in his walk-way.
So, at the moment  this bus is near Kyle; Kyle moves ahead with his walking speed "v" and the next bus, which is now at the
distance L from Kyle, moves toward Kyle with the speed "u". We are given that the next bus will come up to the Kyle new position
in 4 minutes. Hence, we can write the equation for these two bodies, Kyle and the bus, moving toward each other as
L = u*4 + v^4, or L = (u + v)*4, or u + v = this bus is near Kyle; Kyle moves ahead with his walking speed "v" and the next bus, which is now at the
distance L from Kyle, moves toward Kyle with the speed "u". We are given that the next bus will come up to the Kyle new position
in 4 minutes. Hence, we can write the equation for these two bodies, Kyle and the bus, moving toward each other as
L = u*4 + v^4, or L = (u + v)*4, or u + v =  . (1).
This is a standard "Travel and distance equation" for two bodies moving uniformly toward each other.
Indeed, their relative speed (rate) is u+v.
2. Next, let us consider (imagine) walking Kyle on the street and buses that move along the street in the same direction.
Let us consider the very moment . (1).
This is a standard "Travel and distance equation" for two bodies moving uniformly toward each other.
Indeed, their relative speed (rate) is u+v.
2. Next, let us consider (imagine) walking Kyle on the street and buses that move along the street in the same direction.
Let us consider the very moment  when one of the buses on the street comes up to the same position as Kyle in his walk-way.
So, at the moment when one of the buses on the street comes up to the same position as Kyle in his walk-way.
So, at the moment  this bus is near Kyle; Kyle moves ahead with his walking speed "v" and the next bus, which is now at the
distance L behind Kyle, moves in the same direction as Kyle with the speed "u". We are given that the next bus will come up
to the Kyle new position in 12 minutes. Hence, we can write the equation for these two bodies moving in the same direction as
L = u*12 - v^12, or L = (u - v)*12, or u - v = this bus is near Kyle; Kyle moves ahead with his walking speed "v" and the next bus, which is now at the
distance L behind Kyle, moves in the same direction as Kyle with the speed "u". We are given that the next bus will come up
to the Kyle new position in 12 minutes. Hence, we can write the equation for these two bodies moving in the same direction as
L = u*12 - v^12, or L = (u - v)*12, or u - v =  . (2).
This is a standard "Travel and distance equation" for two bodies moving uniformly in the same direction.
Indeed, their relative speed (rate) is u-v.
3. OK. Now we are at the finish line, as I always say in similar situations.
We have two equations (1) and (2) for velocities "u" and "v". Let us write them one more time as a system:
u + v = . (2).
This is a standard "Travel and distance equation" for two bodies moving uniformly in the same direction.
Indeed, their relative speed (rate) is u-v.
3. OK. Now we are at the finish line, as I always say in similar situations.
We have two equations (1) and (2) for velocities "u" and "v". Let us write them one more time as a system:
u + v =  , (1') and
u - v = , (1') and
u - v =  . (2')
Add equations (1') and (2') (both sides). You will get
2u = . (2')
Add equations (1') and (2') (both sides). You will get
2u =  + +  , or 2u = , or 2u = 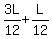 = = 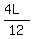 = = 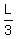 .
Hence, u = .
Hence, u = 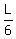 .
What does it mean?
But of course, it means that the time the buses cover the distance L is .
What does it mean?
But of course, it means that the time the buses cover the distance L is  : : 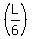 = 6 minutes.
It gives the answer to the problem: the time interval buses leave their terminals is 6 minutes. = 6 minutes.
It gives the answer to the problem: the time interval buses leave their terminals is 6 minutes.
|
|
|