|
Question 1032533: The number of lollies in a jar was divided into 4 lots. The first lot when divided by 9, the second lot when divided by 7, the third lot when divided by 3 and the fourth lot when divide by 5 resulted in the same whole number. What is the least number of lollies that could have been in the jar?
Found 2 solutions by josgarithmetic, robertb:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! MULTIPLE PRODUCTS
1 9 7 3 5
2 18 14 6 10
3 27 21 9 15
4 36 28 12 20
5 45 35 15 25
6 54 42 18 30
7 63 49 21 35
and you can continue this way but it is not always
the most efficient way to find the number in common.
Try this instead:
The list of number lot divisors,
-
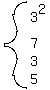
The quantity of lollies is  .
Answer by robertb(5830)  (Show Source):
You can put this solution on YOUR website!
Let w = # of lollies in the 1st lot,
x = # of lollies in the 2nd lot,
y = # of lollies in the 3rd lot,
z = # of lollies in the 4th lot.
The problem is to minimize w + x + y + z.
From the second sentence in the problem, we are given that
 ,
where k is a whole number.
==> w = 9k, x = 7k, y = 3k, and z = 5k.
==> w + x + y + z = 9k + 7k + 3k + 5k = 24k.
Since the minimum value for k is 1, it follows that the least number of lollies that could have been in the jar is  .
|
|
|
| |
