Question 1032522: Hi, these questions are really confusing, could you please help me?
For problems 9 and 10, write each sum using summation notation.
9.2 + 5 + 8 + 11 + ... + 29
10. 6 - 12 + 24 - 48 + ...
11. Find the sum of the arithmetic sequence 2, 4, 6, 8, ..., 70.
12. Find the sum of the geometric sequence
42,7,7/6,...,42,(1/6)^8
For problems 13 and 14, find the sum of the first n terms of the sequence. The sequences are either arithmetic or geometric.
13. -1, 11, -121, ...; n = 9
14. 14, 8, 2,...; n=9
15. Determine whether the infinite series is equal to a real number. If so, find the sum.
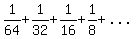
Answer by ikleyn(52775)   (Show Source):
You can put this solution on YOUR website! .
11. Find the sum of the arithmetic sequence 2, 4, 6, 8, ..., 70.
On arithmetic progressions, read the lesson Arithmetic progressions in this site.
The given progression is AP with the first term 2 and the common difference 2.
It contains all even integers between 2 and 70, inclusively.
The number of the terms is 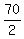 = 35.
Use the formula for the sum of an AP
S =  =  .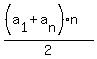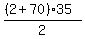
Calculate it yourself.
12. Find the sum of the geometric sequence 42, 7, 7/6,. . . , 42*(1/6)^8
The last term of the progression was written INCORRECTLY. I fixed it.
On geometric progressions, read the lesson Geometric progressions in this site.
The given progression is GP with the first term 42 and the common ratio  .
The number of the terms is 9.
Use the formula for the sum of a GP
S =  =  =  =  =  =  .
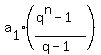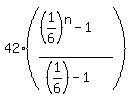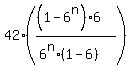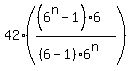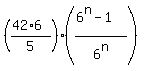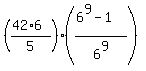Calculate it yourself.
|
|
|
