SOLUTION: There are 32 quarters and dimes in a jar. The total amount in the jar is $5.25. How many of each coin are there?

Algebra ->  Customizable Word Problem Solvers  -> Coins -> SOLUTION: There are 32 quarters and dimes in a jar. The total amount in the jar is $5.25. How many of each coin are there?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1032067: There are 32 quarters and dimes in a jar. The total amount
in the jar is $5.25. How many of each coin are there?
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
There are 32 quarters and dimes in a jar. The total amount
in the jar is $5.25. How many of each coin are there?
There can be no solution with 32 coins.
Perhaps you meant 33 coins instead.  I will
assume so.


Let the number of quarters be x
Let the number of dimes be y


                      Value      Value
Type       Number       of         of
 of          of        EACH       ALL
coin        coins      coin      coins
-------------------------------------------
quarters     x        $0.25     $0.25x
dimes        y        $0.10     $0.10y
-------------------------------------------
TOTALS      33      -----       $5.25

The first equation comes from the "Number of coins" column.

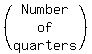
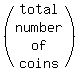  %28matrix%283%2C1%2CNumber%2Cof%2Cquarters%29%29%22%22%2B%22%22%28matrix%283%2C1%2CNumber%2Cof%2Cdimes%29%29%22%22=%22%22%28matrix%284%2C1%2Ctotal%2Cnumber%2Cof%2Ccoins%29%29

                 x + y = 33

 The second equation comes from the last column.
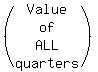
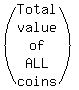  %28matrix%284%2C1%2CValue%2Cof%2CALL%2Cquarters%29%29%22%22%2B%22%22%28matrix%284%2C1%2CValue%2Cof%2CALL%2Cdimes%29%29%22%22=%22%22%28matrix%285%2C1%2CTotal%2Cvalue%2Cof%2CALL%2Ccoins%29%29

         0.25x + 0.10y = 5.25

Get rid of decimals by multiplying every term by 100:

             25x + 10y = 525

 So we have the system of equations:

           system%28x+%2B+y+=+33%2C25x+%2B+10y+=+525%29.

We solve by substitution.  Solve the first equation for y:

           x + y = 33
               y = 33 - x

Substitute (33 - x) for y in 25x + 10y = 525

   25x + 10(33 - x) = 525
    25x + 330 - 10x = 525
          15x + 330 = 525
                15x = 195
                  x = 13 = the number of quarters.

Substitute in y = 33 - x
              y = 33 - (13
              y = 20 dimes.

Checking:  13 quarters is $3.25 and 20 dimes is $2.00
            That's 33 coins.
            And indeed $3.25 + $2.00 = $5.25

Edwin