Question 1031968: Let L:V→W be a linear transformation. Let {(X1),(X2),…, (Xn)} ϵ V. IF {L(X1),L(X2),…, L(Xn)} is linearly dependent, then {X1,X2,...,Xn} is linearly dependent.
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52800)   (Show Source): (Show Source):
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem asks to show that: If {L(X1),L(X2),…, L(Xn)} is linearly dependent, then {X1,X2,...,Xn} is linearly dependent.
It would be easier to prove the contrapositive of this statement:
If {X1,X2,...,Xn} is linearly independent, then {L(X1),L(X2),…, L(Xn)} is linearly independent as well. This is quite easy to prove.
DEFINITION: Let 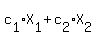 +...+ +...+ , where , where 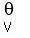 is the zero vector in V. is the zero vector in V.
Then linear independence of the set implies that only  = ...= = ...=  will satisfy the previous equation. will satisfy the previous equation.
Now let
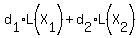 +...+ +...+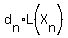 = =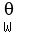 <-----Equation A. <-----Equation A.
(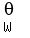 is the zero vector in W and the d constants are arbitrary.) is the zero vector in W and the d constants are arbitrary.)
By the property of the linear transformation L,
Equation A is equivalent to
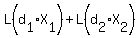 +...+ +...+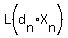 ) = ) =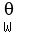 , or , or
L( +...+ +...+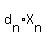 ) = ) =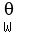 . .
==>  +...+ +...+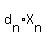 = = 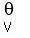 , ,
or the left-hand side linear combination would be an element of the kernel of L.
==>  =...= =...= , ,
by virtue of the linear independence of the X vectors.
Therefore, {L(X1),L(X2),…, L(Xn)} is linearly independent as well, and the theorem is proved.
|
|
|