SOLUTION: What is the coefficient of x in (x^4 + x^3 + x^2 + x + 1)^4?

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: What is the coefficient of x in (x^4 + x^3 + x^2 + x + 1)^4?      Log On


   

Question 1031691: What is the coefficient of x in (x^4 + x^3 + x^2 + x + 1)^4?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
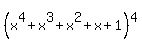
%28x%5E4+%2B+x%5E3+%2B+x%5E2+%2B+x+%2B+1%29%5E4%22%22=%22%22



The only way to get a x in that multiplication is: 

1. When the 1's in the 1st, 2nd, and 3rd parentheses are multiplied 
   by the x in the 4th parentheses, giving term 1*1*1*x = x.

2. When the 1's in the 1st, 2nd, and 4th parentheses are multiplied 
   by the x in the 3rd parentheses, giving term 1*1*x*1 = x.

3. When the 1's in the 1st, 3rd, and 4th parentheses are multiplied 
   by the x in the 2nd parentheses, giving term 1*x*1*1 = x.

4. When the 1's in the 2nd, 3rd, and 4th parentheses are multiplied 
   by the x in the 1st parentheses, giving term x*1*1*1 = x.

So the only term in x is x+x+x+x = 4x, which has coefficient 4.

Incidentally, the whole thing multiplied out is:

x16+4x15+10x14+20x13+35x12+52x11+68x10+80x9+85x8+80x7+68x6+52x5+35x4+20x3+10x2+4x+1

Edwin