Consider the graph y=(x-k)^2 where k is any integer. What effect does changing the value of have on:
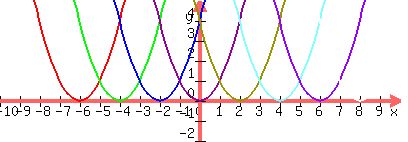
The red graph is for k=-6
The green graph is for k=-4
The dark blue graph is for k=-2
The wine-colored graph is for k=0
The green and yellow graph is for k=2
The light blue graph is for k=4
The purple graph is for k=6
The axis of symmetry
The axis of symmetry is always the vertical line through
the turning point and its equation is x=k
The turning point
The turning point always the point (k,0)
The x and y intercepts
The x intercept is the vertex (k,0)
The y-intercept is the point (0,k2)
The shape of the curve
The curve always has the same shape
Edwin